斯坦福21秋季:实用机器学习学习笔记
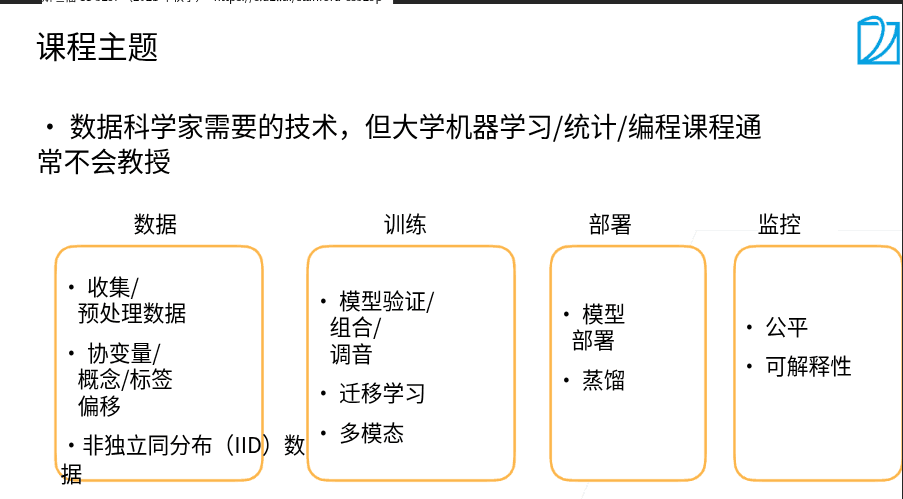
1.1 课程介绍
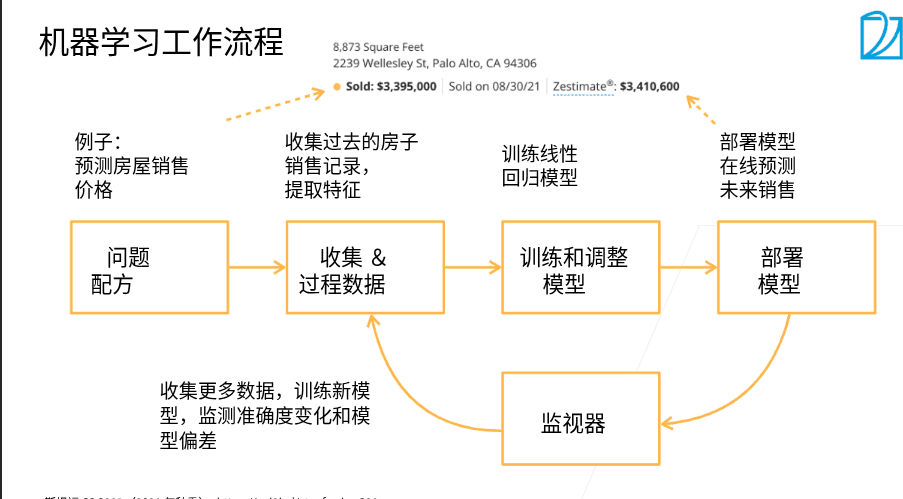
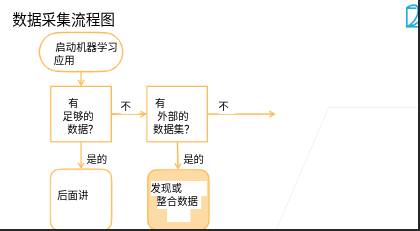
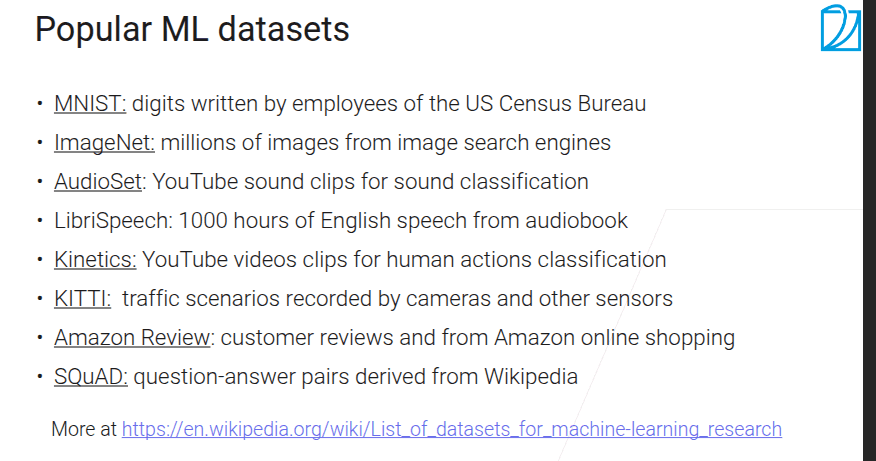
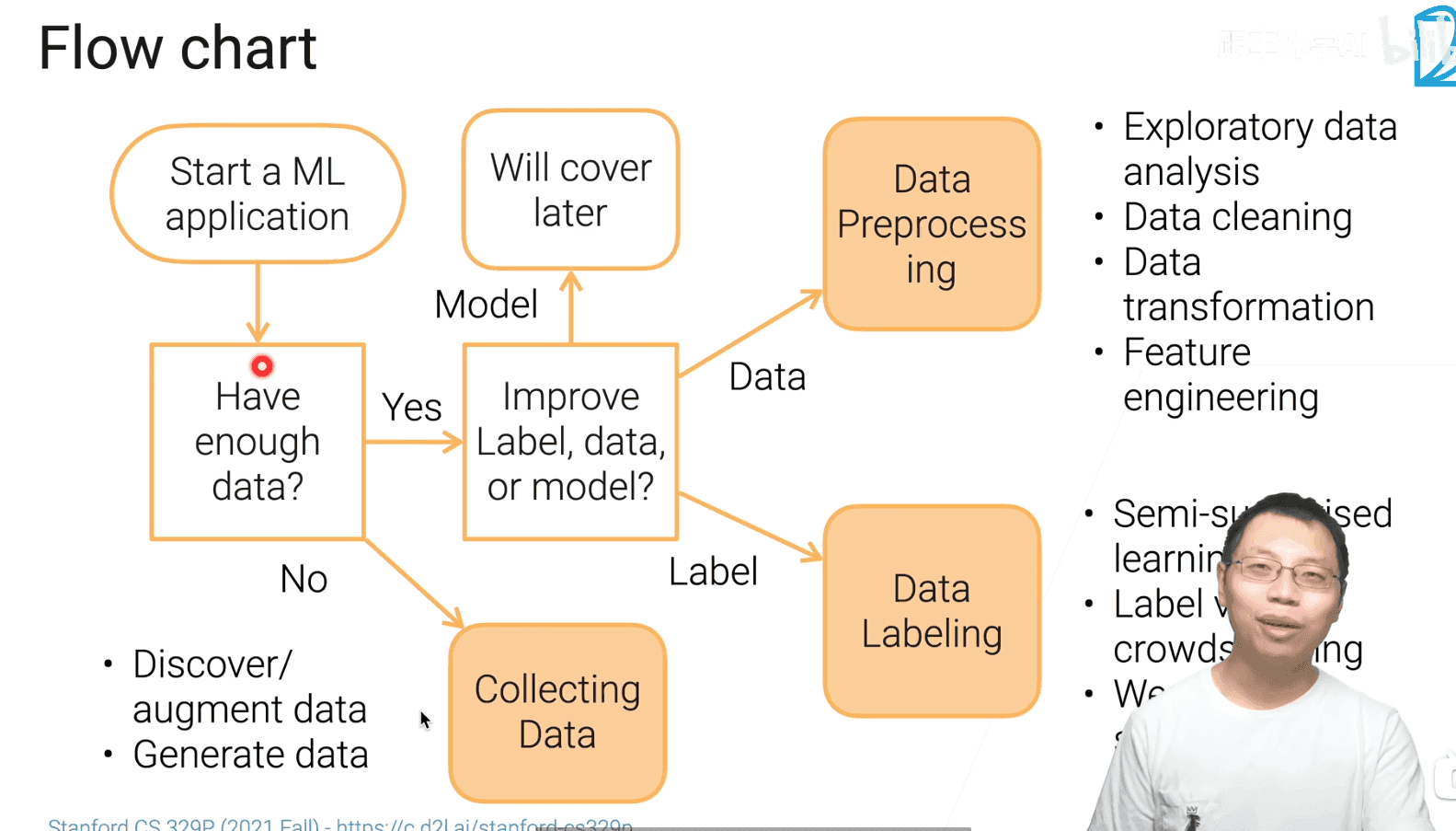
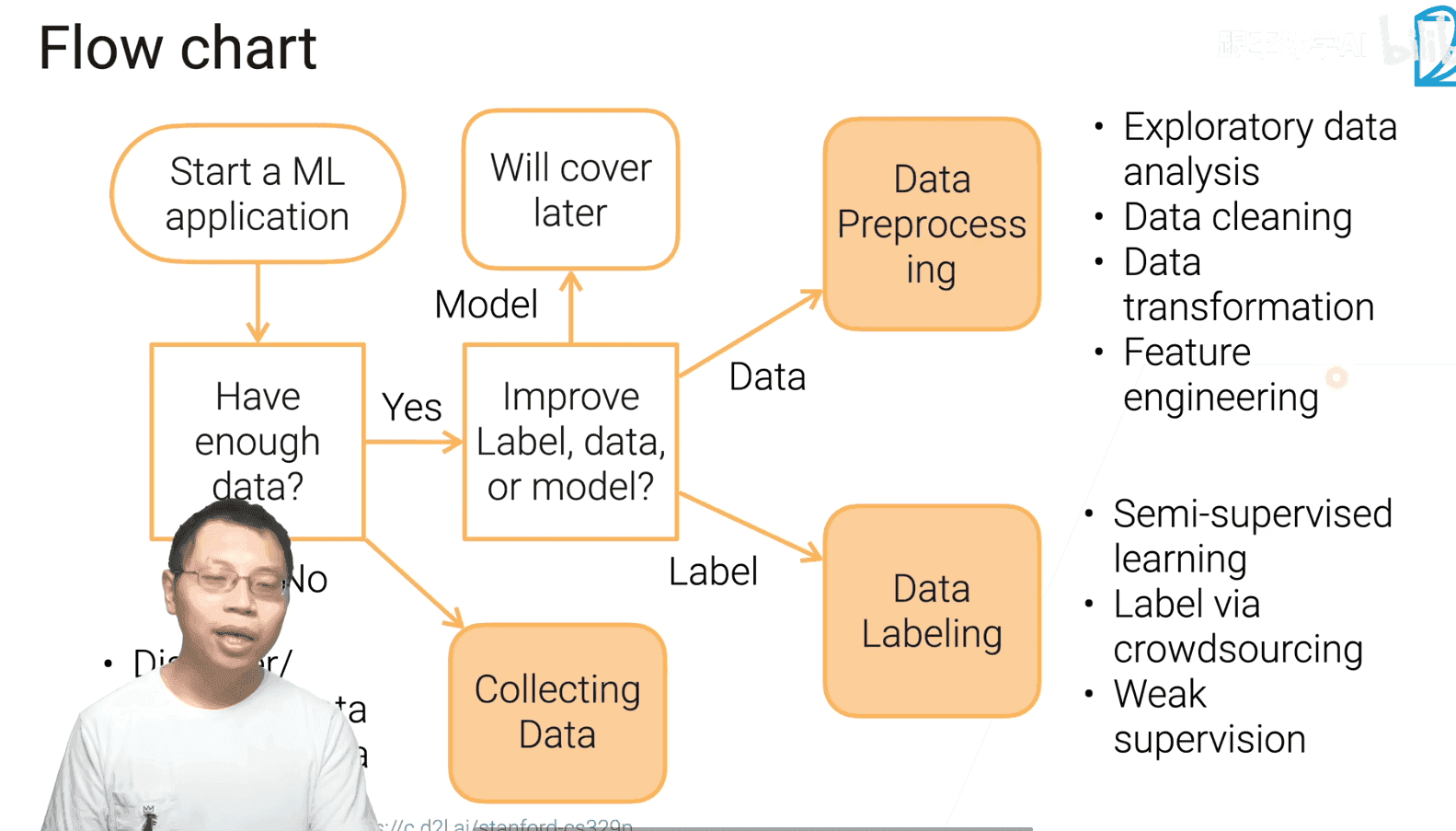
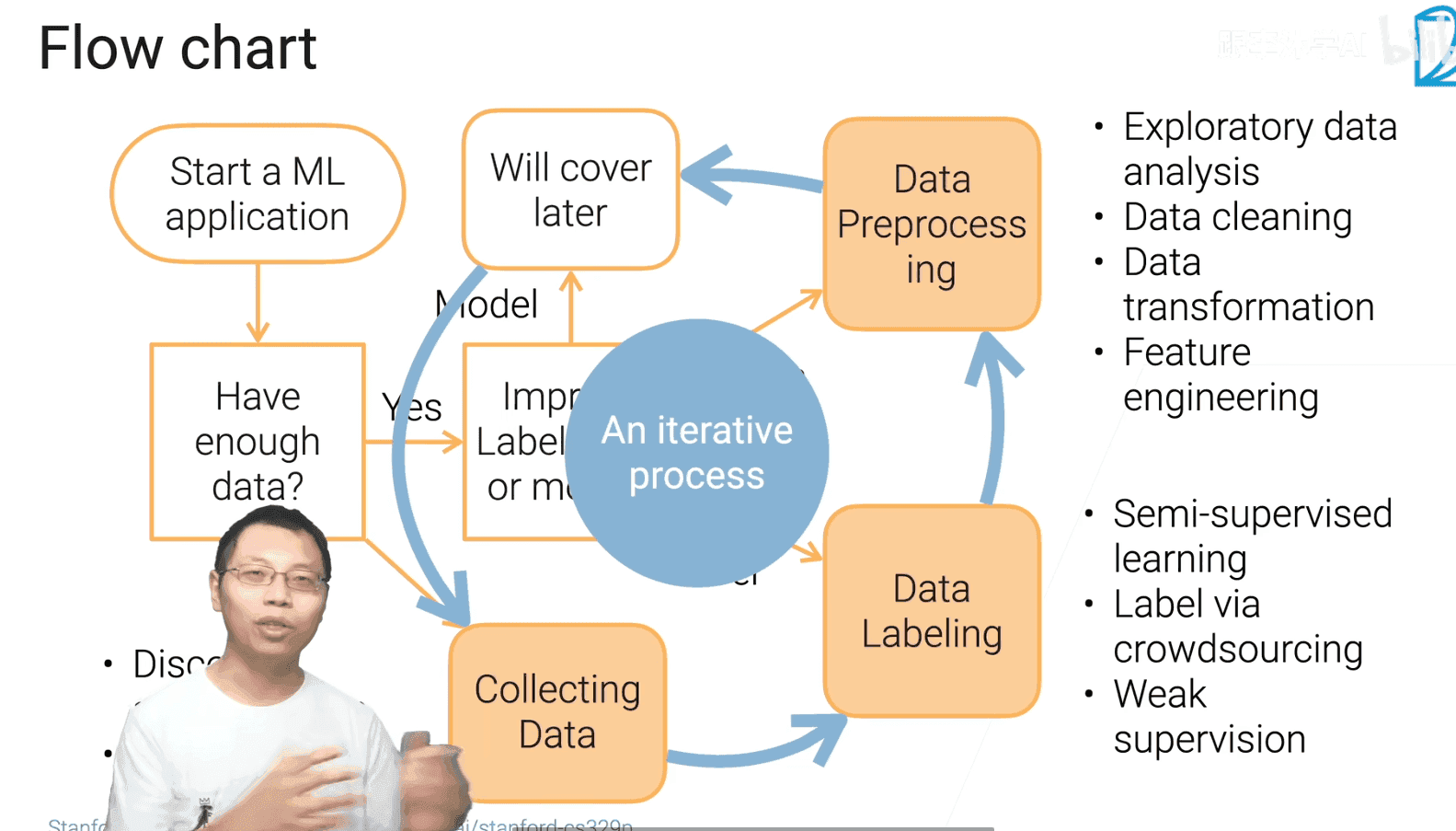
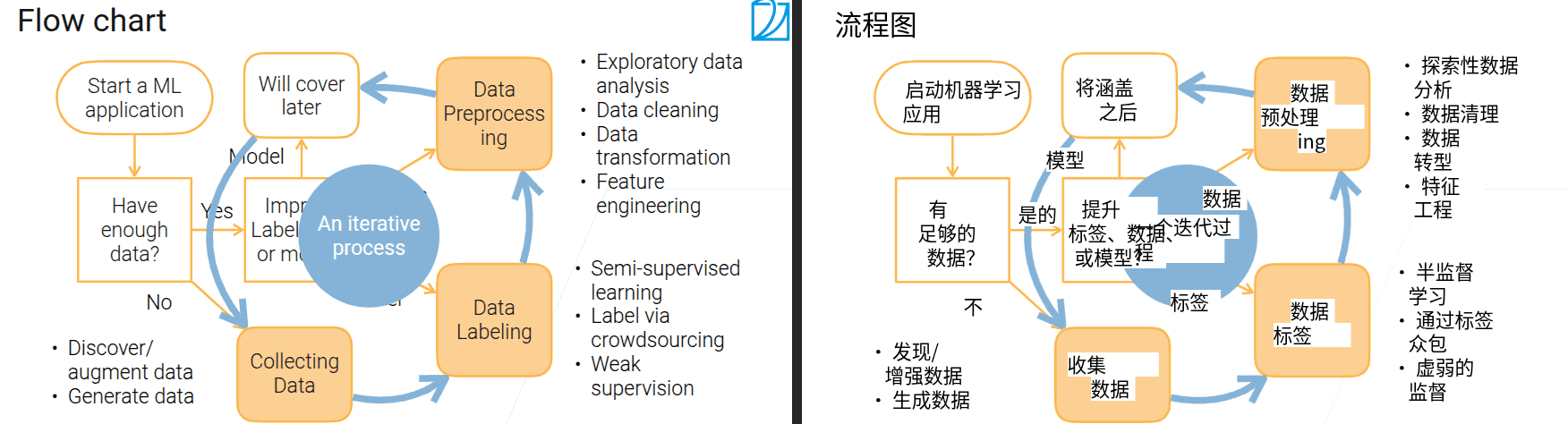
1.2 数据获取
- 最首要的步骤是将具体的问题转换为机器学习的问题
1.3 网页数据抓取
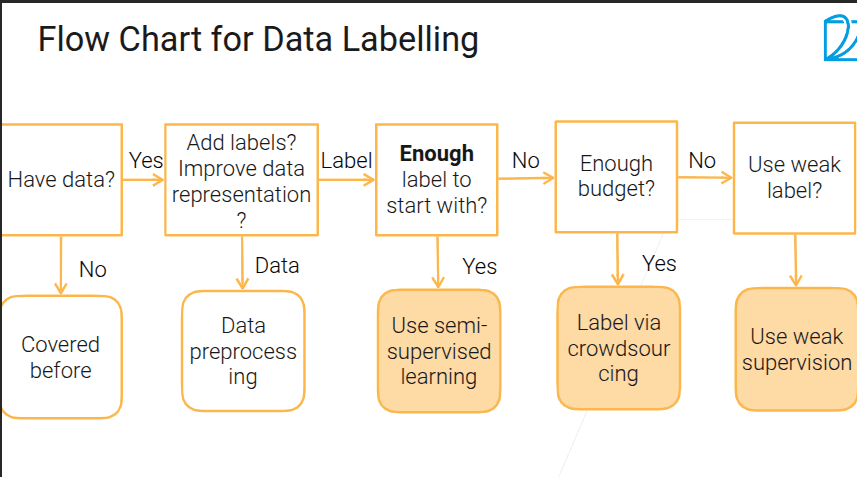
1.4 数据标注
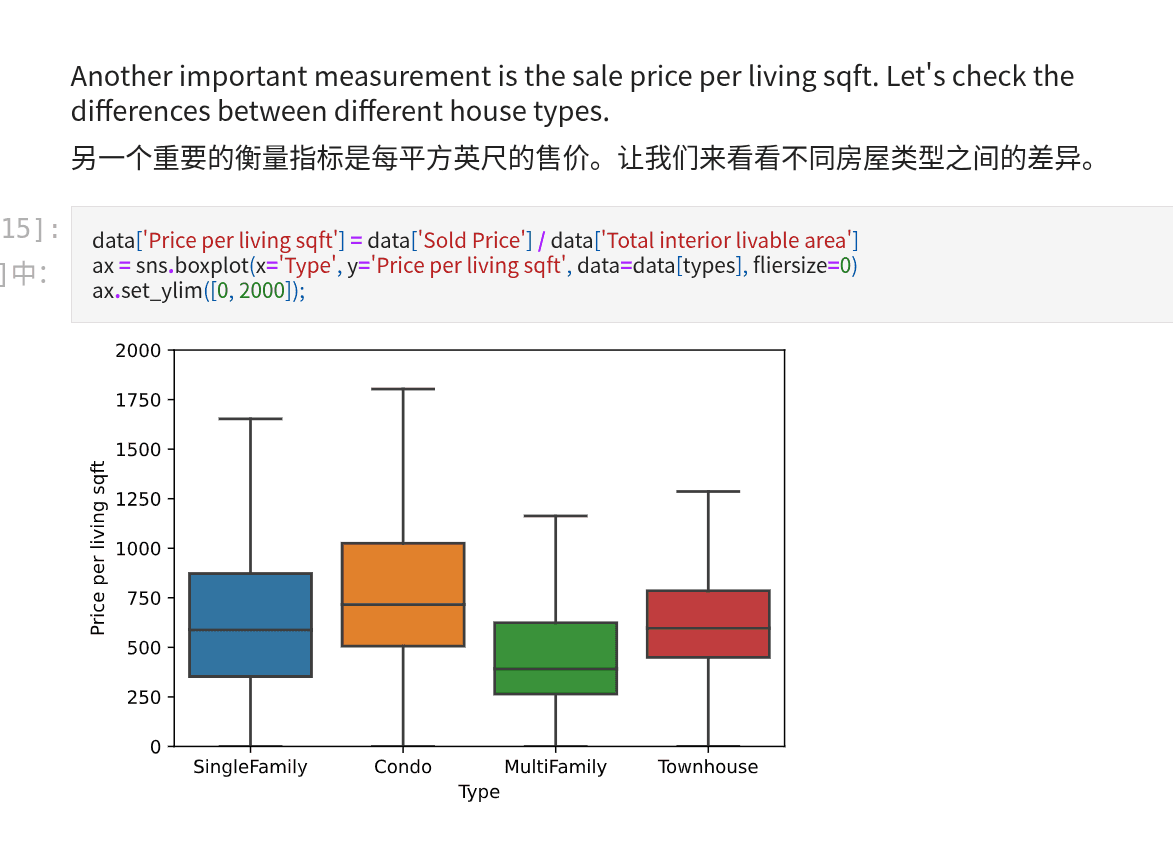
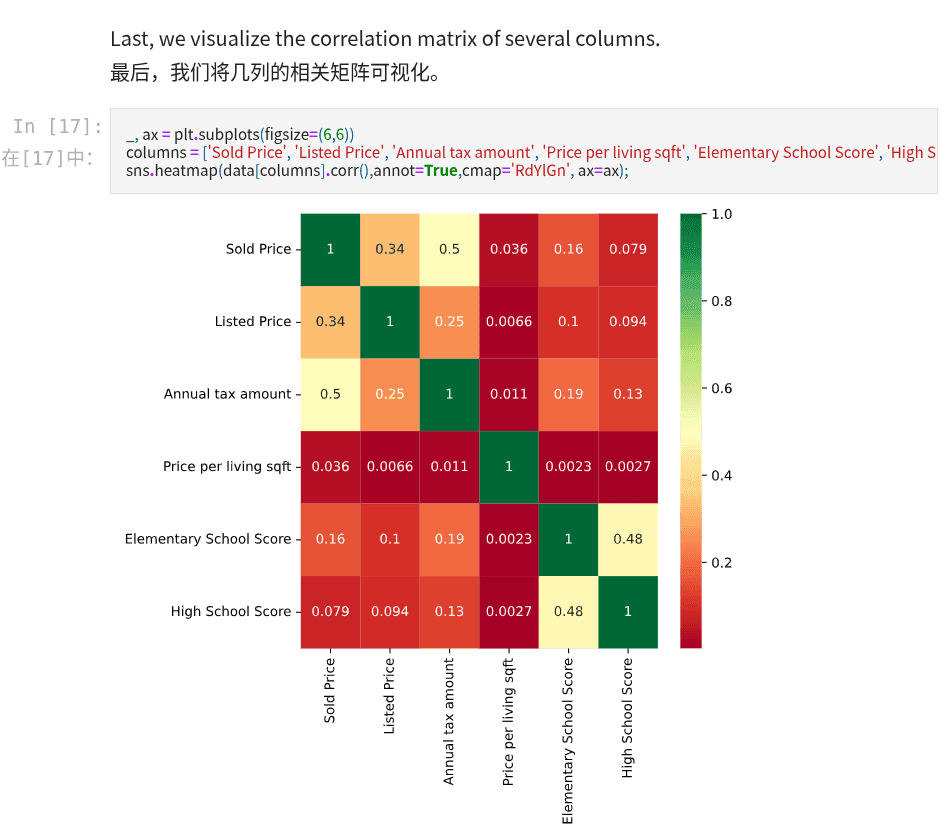
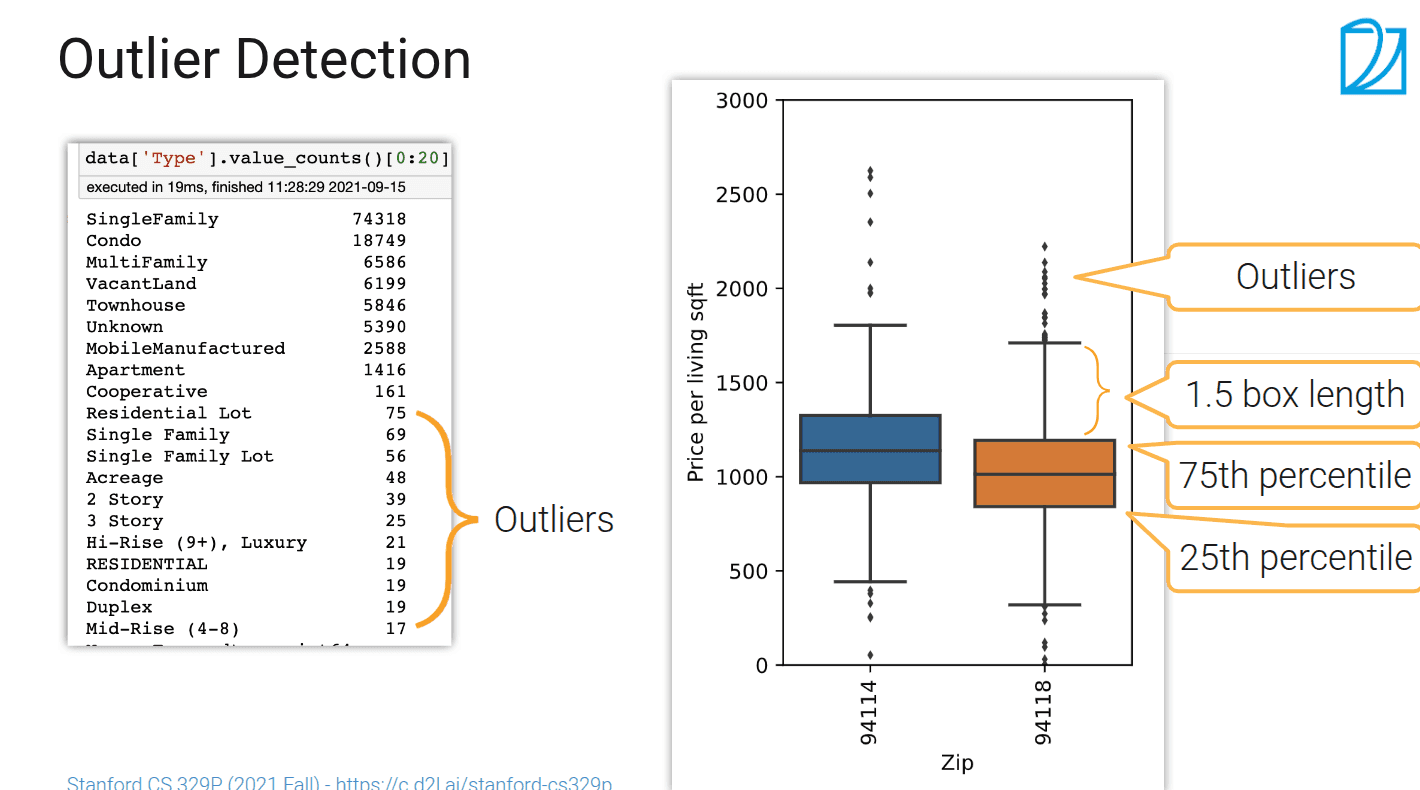
2.1 探索性数据分析
- matplotlib 画图 可视化
- seaborn 基于matplotlib 进阶画图
-
pandas 等这些包可以直接读压缩文件,数据可以不解压。对文本等好用,图片类数据不推荐,因为已经进行了比较好的压缩
这段代码是 pandas 中用于数据清洗的常见操作,主要目的是筛选出缺失值比例低于 30% 的列。
具体解释如下:
1. `null_sum = data.isnull().sum()`
- `data.isnull()` 会生成一个与原数据结构相同的布尔值 DataFrame,其中缺失值位置为 True,非缺失值为 False
- `.sum()` 对这些布尔值求和(True 计为 1,False 计为 0),得到每列的缺失值总数
2. `data.columns[null_sum < len(data) * 0.3]`
- `len(data)` 是数据的总行数
- `len(data) * 0.3` 计算出总数据量的 30% 作为阈值
- `null_sum < len(data) * 0.3` 生成一个布尔索引,标记哪些列的缺失值数量低于总数据量的 30%
- 最终返回所有满足"缺失值比例 < 30%"条件的列名
这段代码的作用是筛选出缺失值较少(低于 30%)的列,通常用于数据预处理阶段,决定哪些列适合保留进行后续分析(而不是因为缺失值太多而直接删除整列)。
- 数据类型为 object , 一般是纯文本
- data.discribe()可以透视全表的统计信息
-
data = data[~abnormal]是 pandas 中常用的 “数据清洗” 操作,通过布尔索引的取反,快速过滤掉标记为 “异常” 的行,保留正常数据。这种写法简洁高效,是处理异常值、筛选数据的典型技巧。
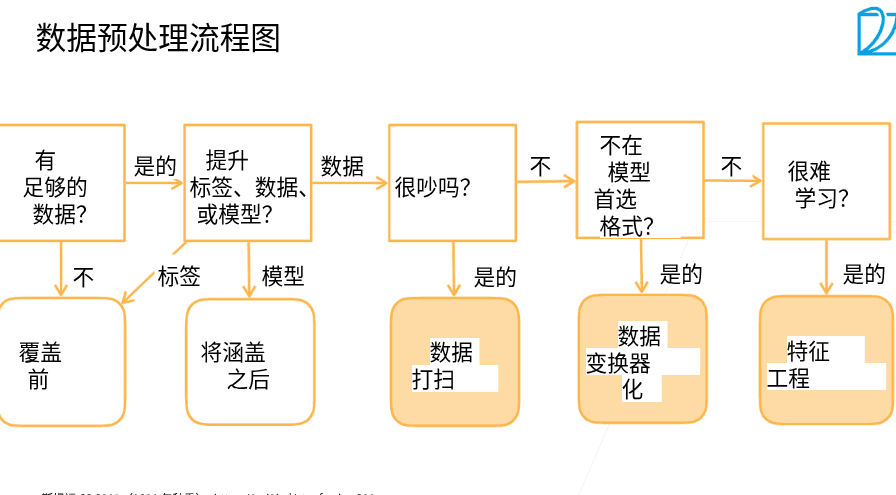
2.2 数据清理
2.3 数据变换
- 需要平衡数据质量、存储大小、读取速度
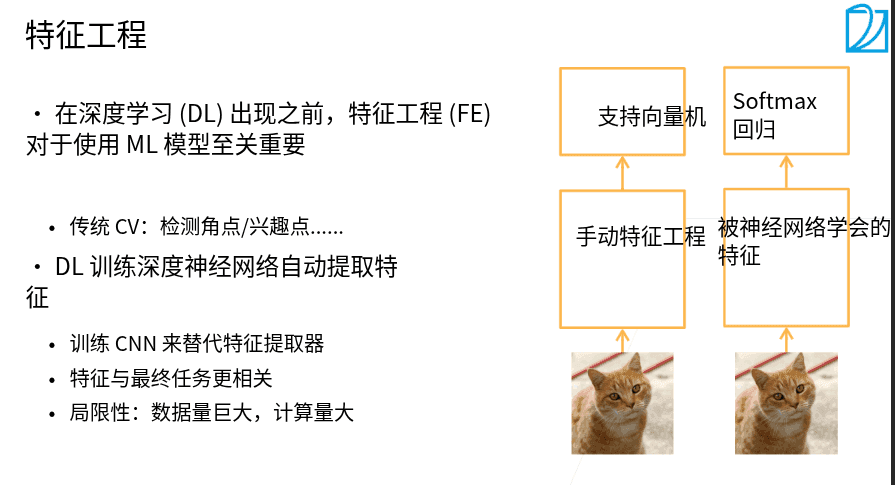
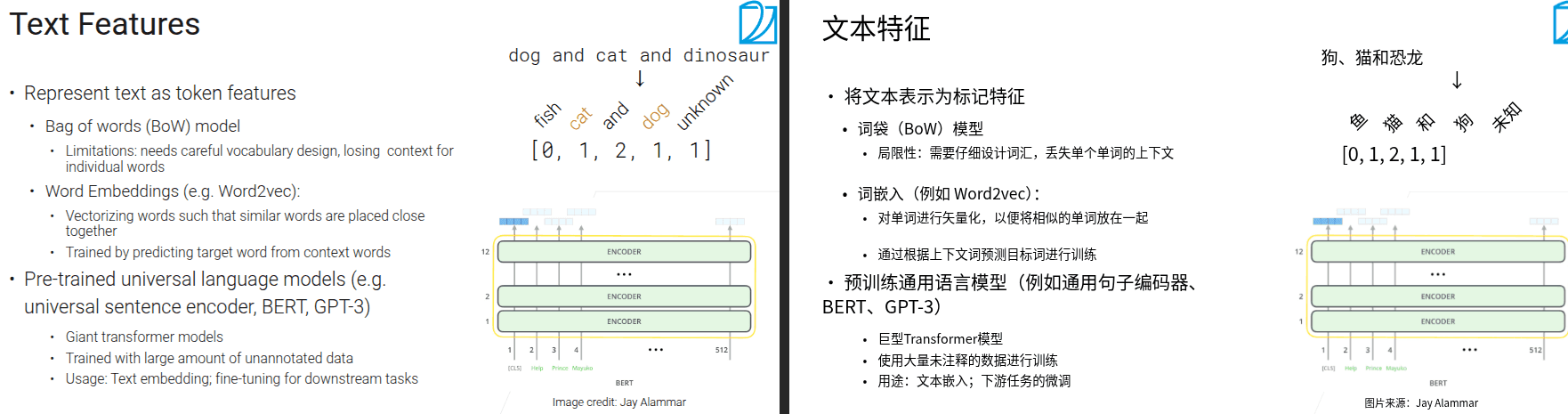
2.4 特征工程
- 特征工程通过对原始数据的清洗、转换、构造、筛选,将其加工成更能反映问题本质、适配模型学习逻辑的特征,从而提升模型效果。
-
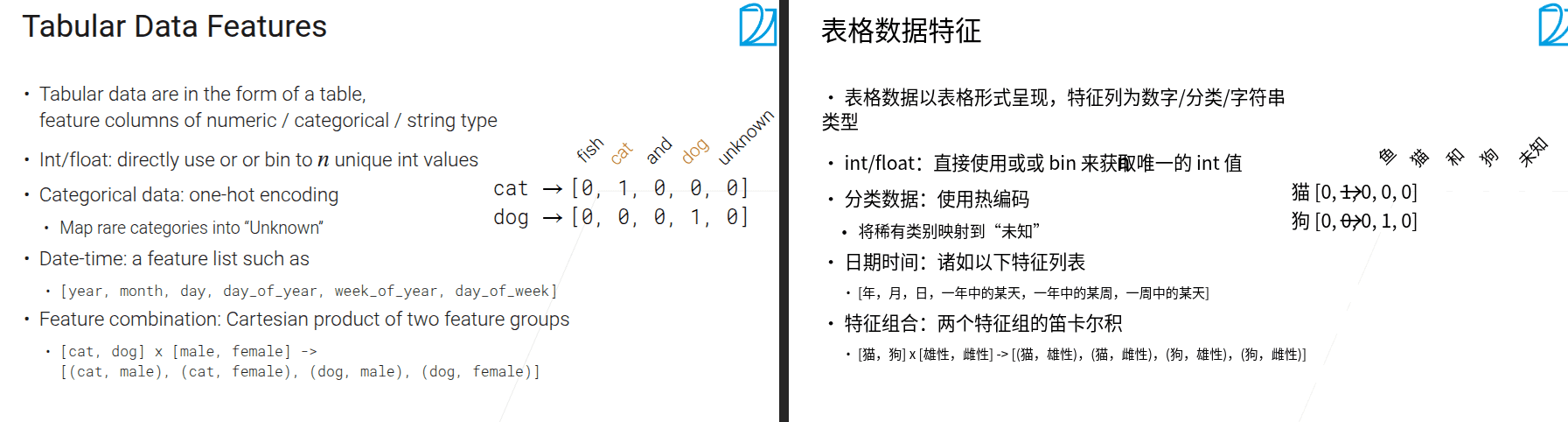
这句话的意思是:对于整数(int)或浮点数(float)类型的数据,可以直接使用这些数值,或者对其进行分箱(binning)处理,将其划分成\(n\)个不同的整数数值。
简单解释一下,“directly use”就是直接使用原始的整数或浮点数;“bin to \(n\) unique int values”是指分箱操作,比如把一系列连续的数值(像年龄,有20、25、30等),按照一定规则分成\(n\)个区间,每个区间对应一个唯一的整数值(比如把20 - 29岁归为1,30 - 39岁归为2等,这里\(n\)可能是2,代表两个区间对应的整数值),这样能将连续型数据转化为离散型的整数类别数据,方便后续处理或模型使用。
- 将长尾内容全部映射为未知
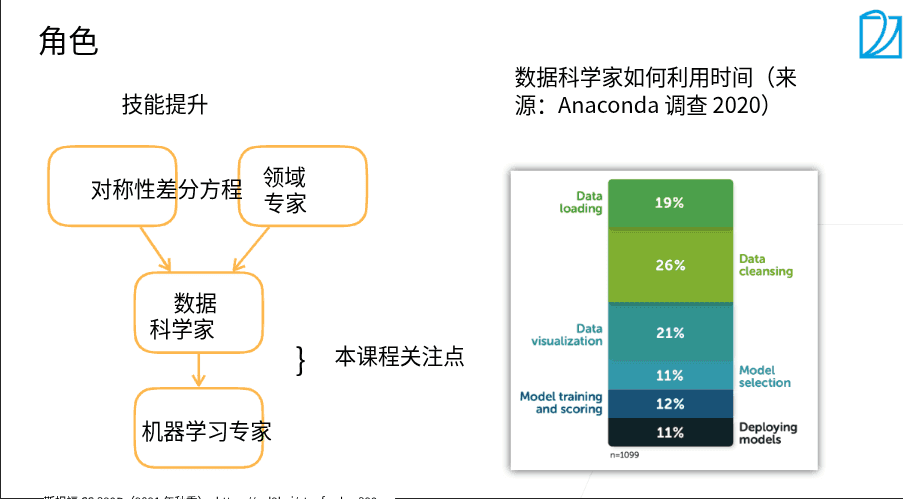
2.5 数据科学家的日常
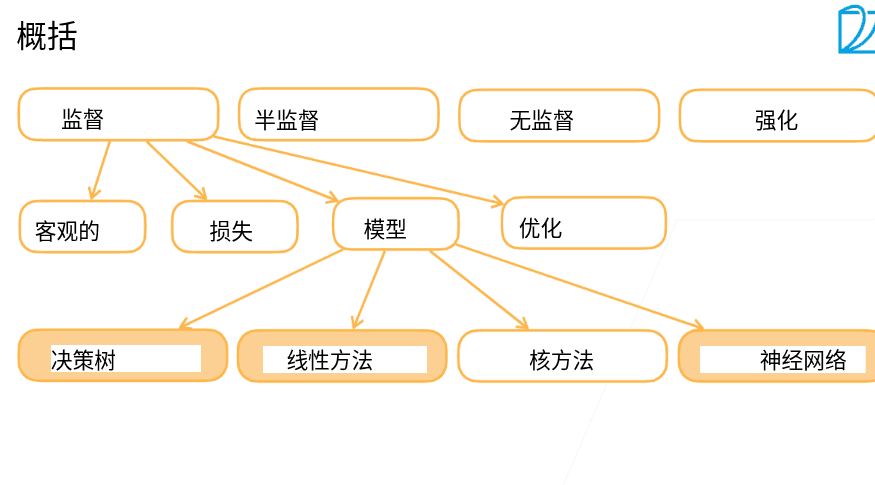
3.1 8分钟机器学习介绍
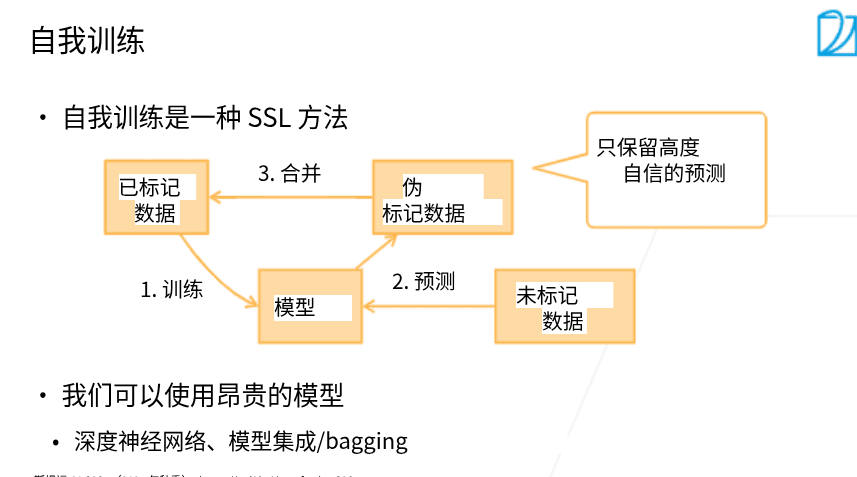
- 自训练 在已有标号的数据上训练一个模型,用于预测没有标注的数据,保留置信度高的数据,重复这个过程
- 密度估计(Density Estimation)简要介绍(GAN)
密度估计是机器学习与统计学的核心任务之一,目标是从有限的观测数据中,推断出数据背后真实的概率分布(概率密度函数,Probability Density Function, PDF)。它回答了 “数据在不同取值区域的‘密集程度’如何” 这一问题,是后续数据分析(如异常检测、聚类、生成模型)的基础。
- 强化学习 通过环境的反馈进行最大化奖励,像人类的学习方式

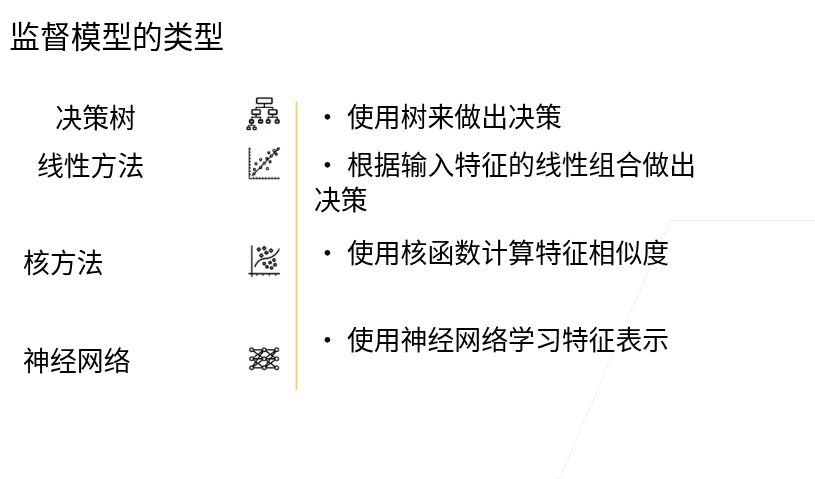
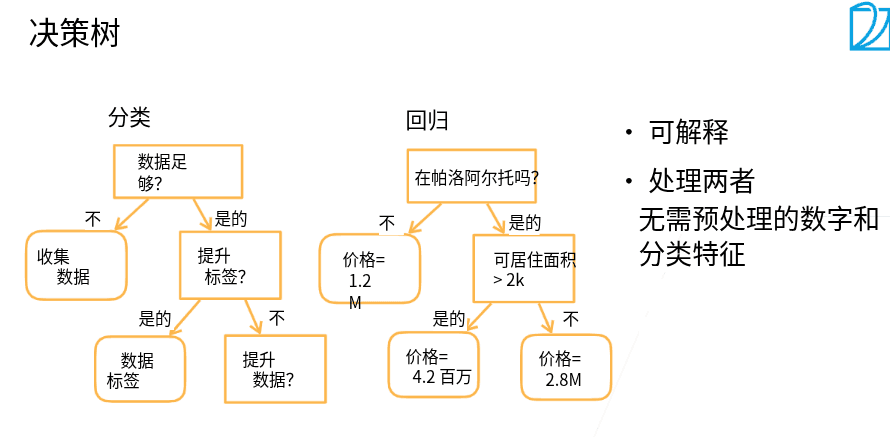
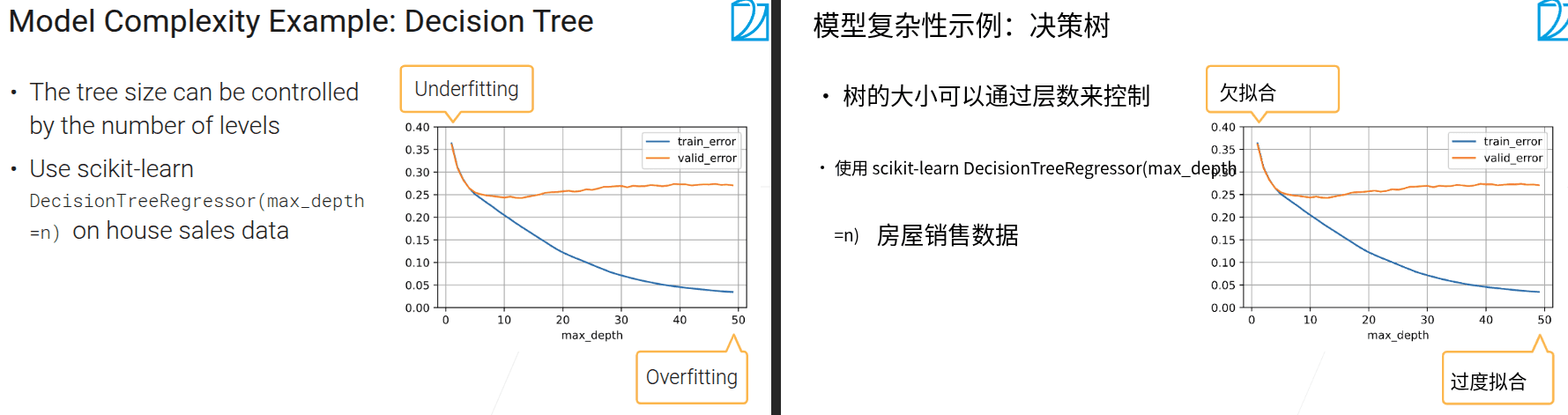
3.2 最简单也最常用的决策树
- 优点 -可解释性
- 可以处理数值型和类别型的特征
- 缺点
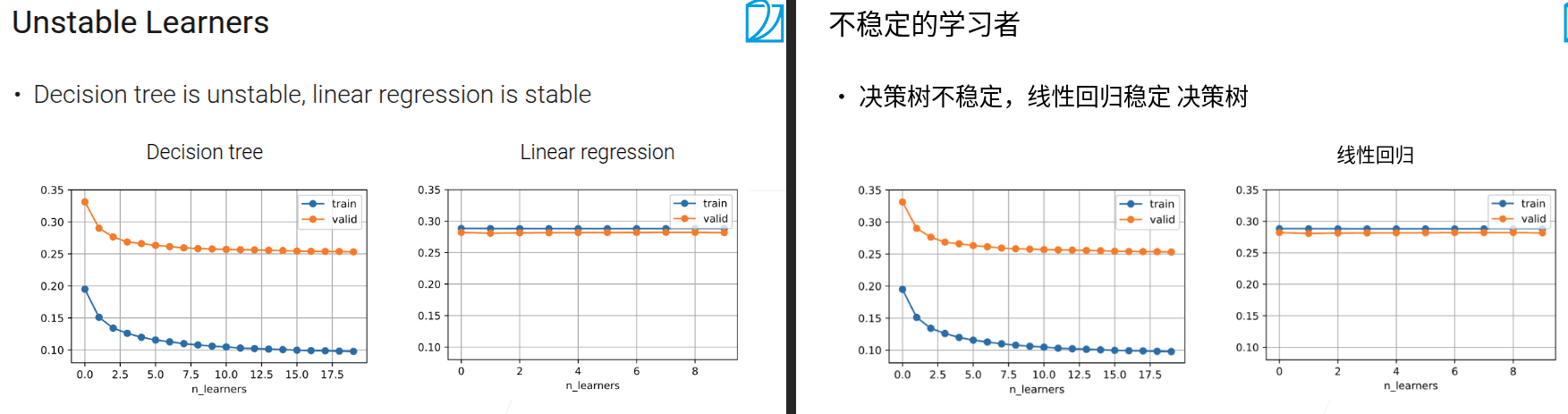
- 非常不稳定(集成学习
- 过拟合(剪枝
-
随机森林为什么叫随机森林
- bagging 随机采样,可以有重复
-
基于梯度的Boosting
- 顺序的训练,一起合成一个大的模型
- 后续的训练是做残差,使模型不断逼近真实值(类似梯度下降
-
如果我们用均方误差(Mean Square Error,MSE)作为损失函数(衡量预测值和真实值差距的函数),数学上可以推导得出:此时 “残差”\(y_i - F_t(x_i)\),恰好等于损失函数对\(F_t(x)\)的负梯度\((-\frac{\partial L}{\partial F}\))。这意味着:用残差去训练新树,本质上是在沿着 “损失函数下降最快的方向(梯度方向)” 去优化模型—— 就像 “梯度下降” 算法找最优解的思路一样。所以这种方法被称为 “梯度提升”(Gradient Boosting)。 简单总结:GBDT 通过 “顺序训练决策树,每棵新树拟合前序模型的残差(或损失的负梯度),再累加所有树” 的方式,逐步把预测效果提升到很好,而 “梯度” 的特点体现在 “用损失的梯度方向指导新树学习” 这一点上

-
树模型的最大问题是不稳定,对噪音敏感;用很多树放在一起来降低偏移和方差
- 树模型的结果都还不错,可以当做一个开始

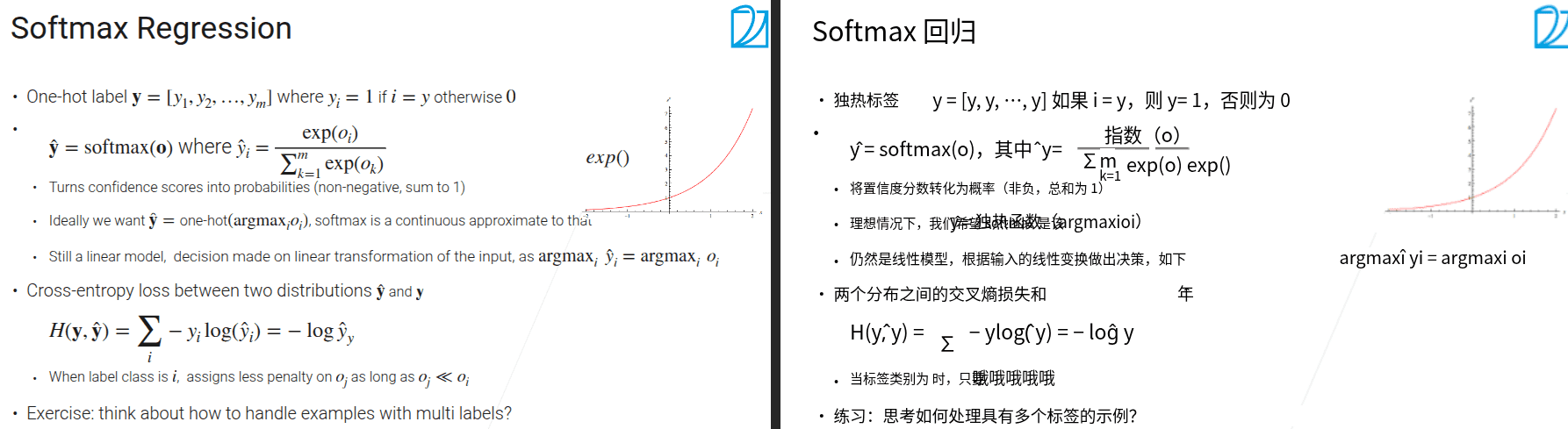
3.3 最简单也同样最常用的线性模型
3.4 随机梯度下降
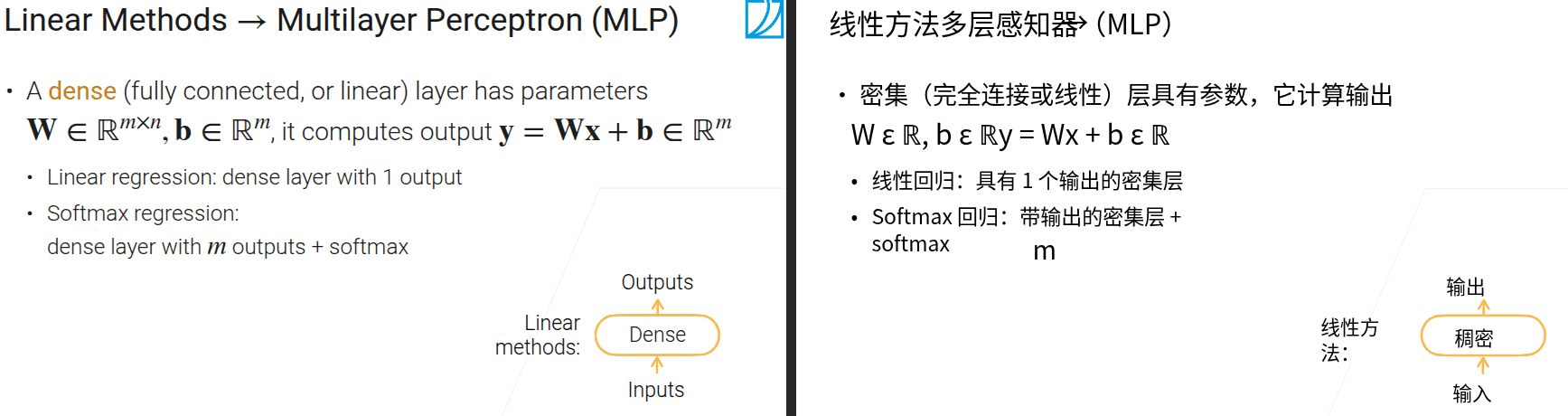
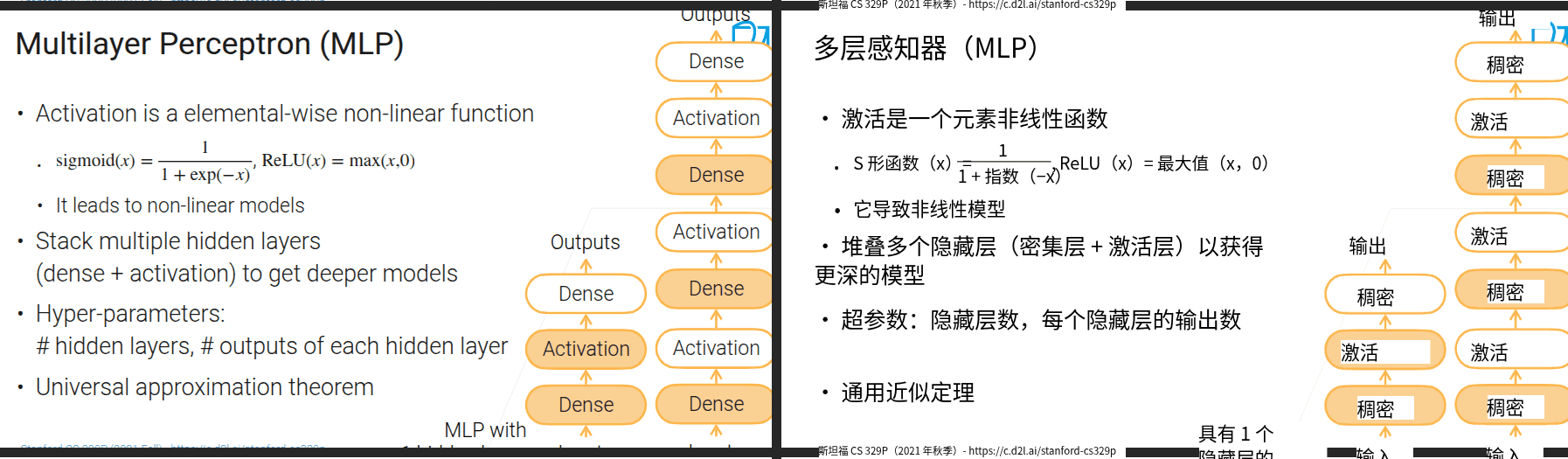
3.5 多层感知机
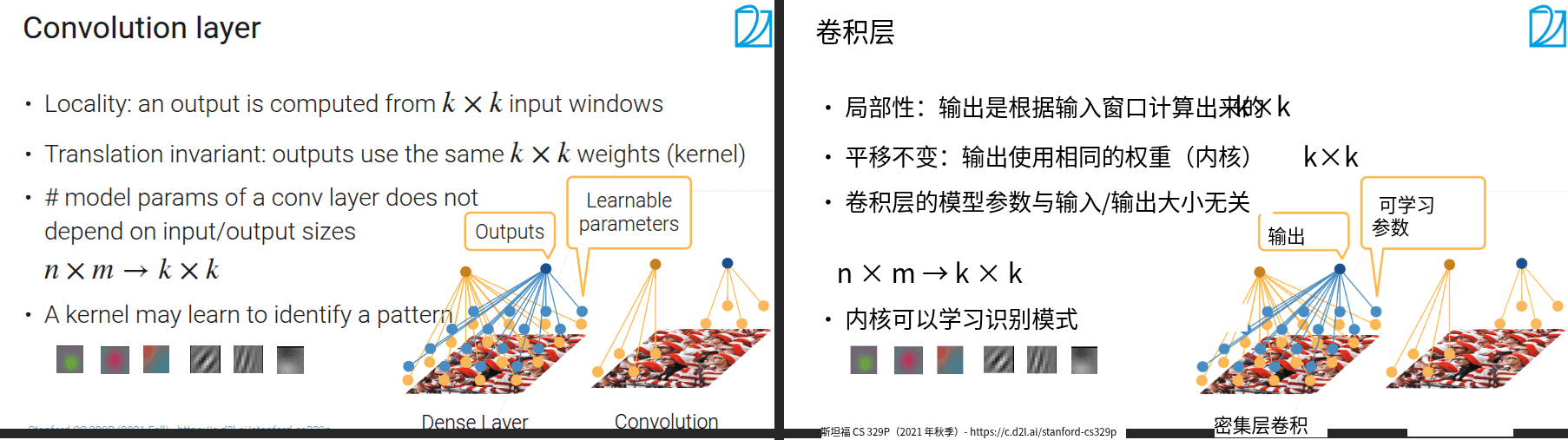
3.6 卷积神经网络
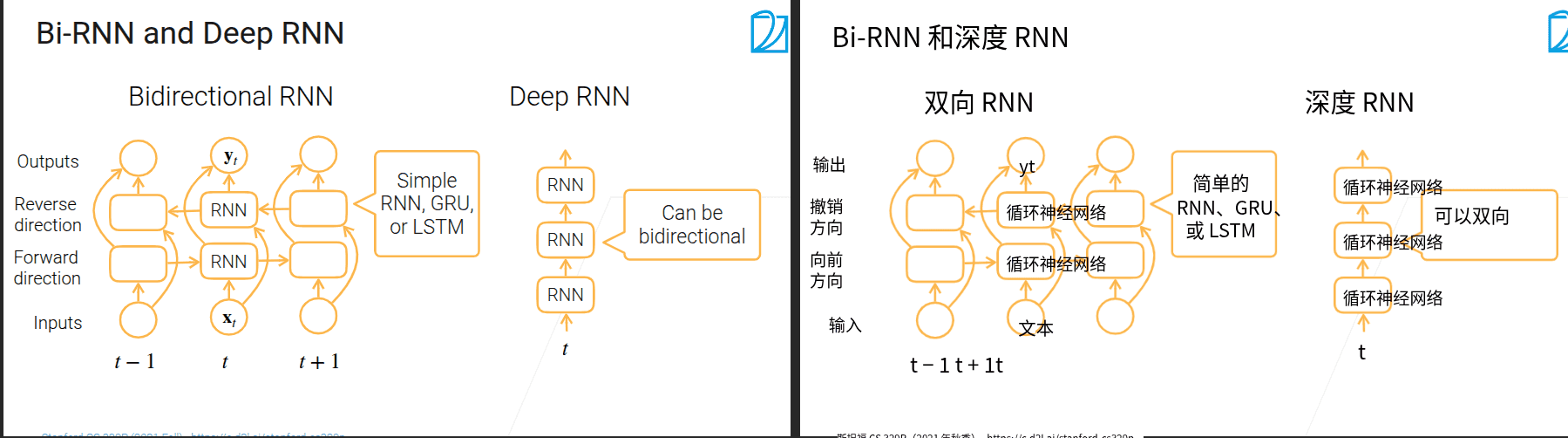
3.7 循环神经网络
- 问题
- 全连接的输入维度不能发生变化
-
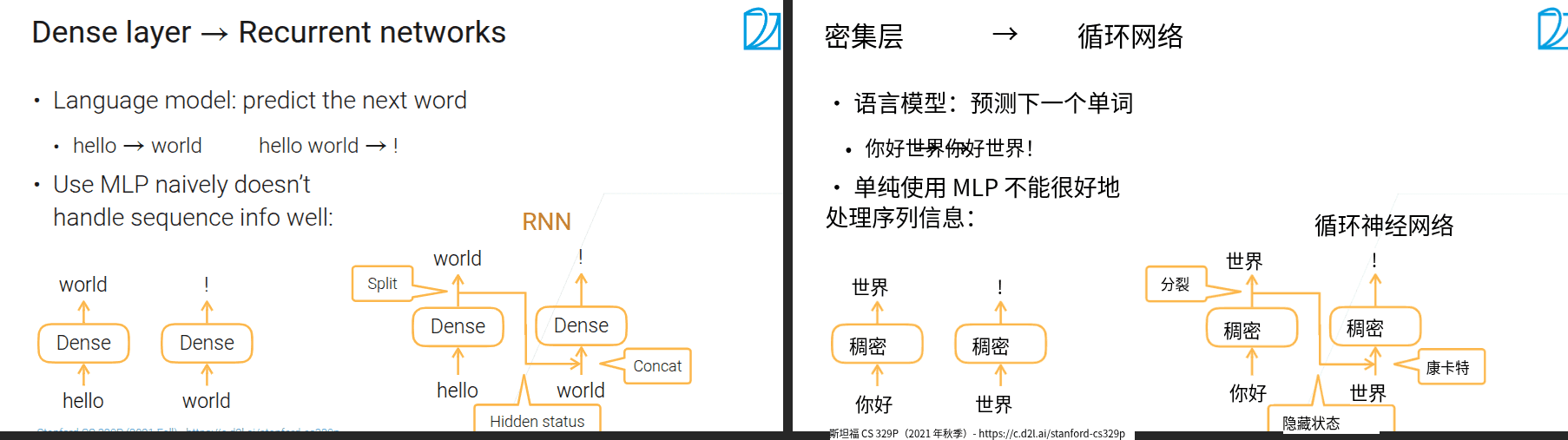
H和当前的输入一起concat进入当前卷积层,H来自上一层的卷积没经过softmax的输出。一直这样循环,H中会包含之前的所有信息
-
\(h_t\) 和\(y_t\)本质上是一个东西(对简单的RNN来说
- 通过权重来判断需要抑制什么

RNN 输入形状(Shape)解释
我们用一个更具体的“文本情感分类”例子,把这三个参数和实际数据对应起来,你就能一目了然了:
假设我们有这样一批影评数据(共2条,作为一个batch):
- 第一条影评:"这部电影太精彩了,强烈推荐!"(含7个词)
- 第二条影评:"剧情拖沓,演员演技差,不建议看。"(含8个词)
1. num_steps(时间步/序列长度)
- 含义:每个样本(单条影评)被统一处理成固定长度的词序列,这个固定长度就是num_steps。
- 例子:
上面两条影评的词数分别是7和8,我们可以设定num_steps=10(选一个比最长样本稍大的值)。
对第一条影评(7个词):用<PAD>(填充符)补3个位置,变成10个词的序列。
对第二条影评(8个词):用<PAD>补2个位置,也变成10个词的序列。
此时,num_steps=10就代表“每个样本都被处理成10个词的序列”。
2. batch_size(批大小)
- 含义:一次同时输入给模型的样本数量(同时处理多少条影评)。
- 例子:
我们上面有2条影评,如果一次把这2条都输入模型,那么batch_size=2。
实际训练中,这个值通常设为32、64等(根据硬件能力调整),比如batch_size=32就代表“每次同时处理32条影评”。
3. num_inputs(特征维度)
- 含义:每个词被转换成的向量的维度(每个词用多少个数字表示)。
- 例子:
我们用Word2Vec或BERT给每个词生成词向量,假设用300维的向量(每个词用300个数字描述),那么num_inputs=300。
比如“精彩”这个词可能被表示为[0.21, 0.56, ..., -0.32](共300个数字)。
最终输入shape
把上面三个参数组合起来,输入给RNN的shape就是 (num_steps, batch_size, num_inputs):
- 对我们的例子:
(10, 2, 300)
可以理解为:“有2条影评,每条影评有10个词,每个词用300维的向量表示”。
为什么这样设计?
RNN需要按时间步逐个处理词:
- 第1个时间步:处理2条影评的第1个词(每个词是300维向量)
- 第2个时间步:处理2条影评的第2个词,同时结合上一步的“记忆”
- ...
- 第10个时间步:处理完所有词,此时模型已经“读完”了所有影评内容,最后输出情感判断结果。
这样是不是就清晰多了?这三个参数本质上是为了让模型能有条理地“逐词阅读”一批文本
4.1 模型评估
把具体的事件看成一个分布P,对其采样可以得到data,训练得到一个模型。我们需要的是模型的泛化能力,需要
- 采样方法
- 模型超参数
-
不关心对负类的预测
-
曲线下面积叫做AUC
- TP turePositive;FN falseNegative
- AUC=1特别好;AUC=0.5完全分不开。任务是把AUC从0.5拉到1
- AUC关注的是区分度,只关心相对排序,不关心绝对值
- ROC 曲线越靠近左上角,说明模型在区分正、负类时的性能越好。横轴是假正例率(FPR)、纵轴是真正例率(TPR)
- 要注意右图是一个比值。y\x 越大,曲线下面积越大,某一项比例越高

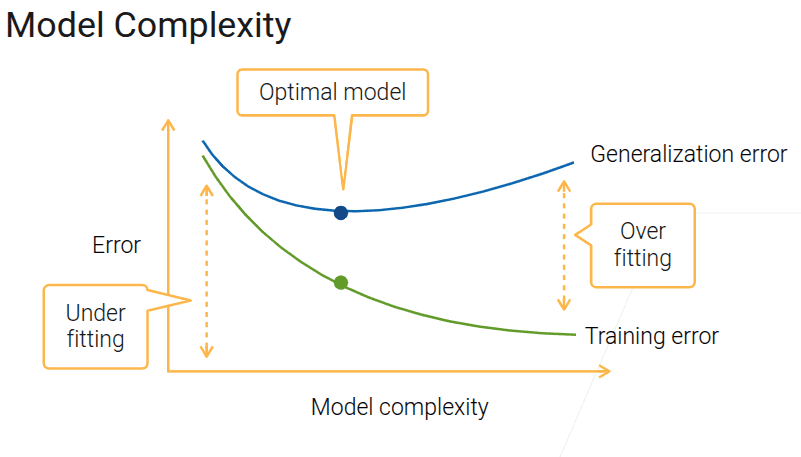
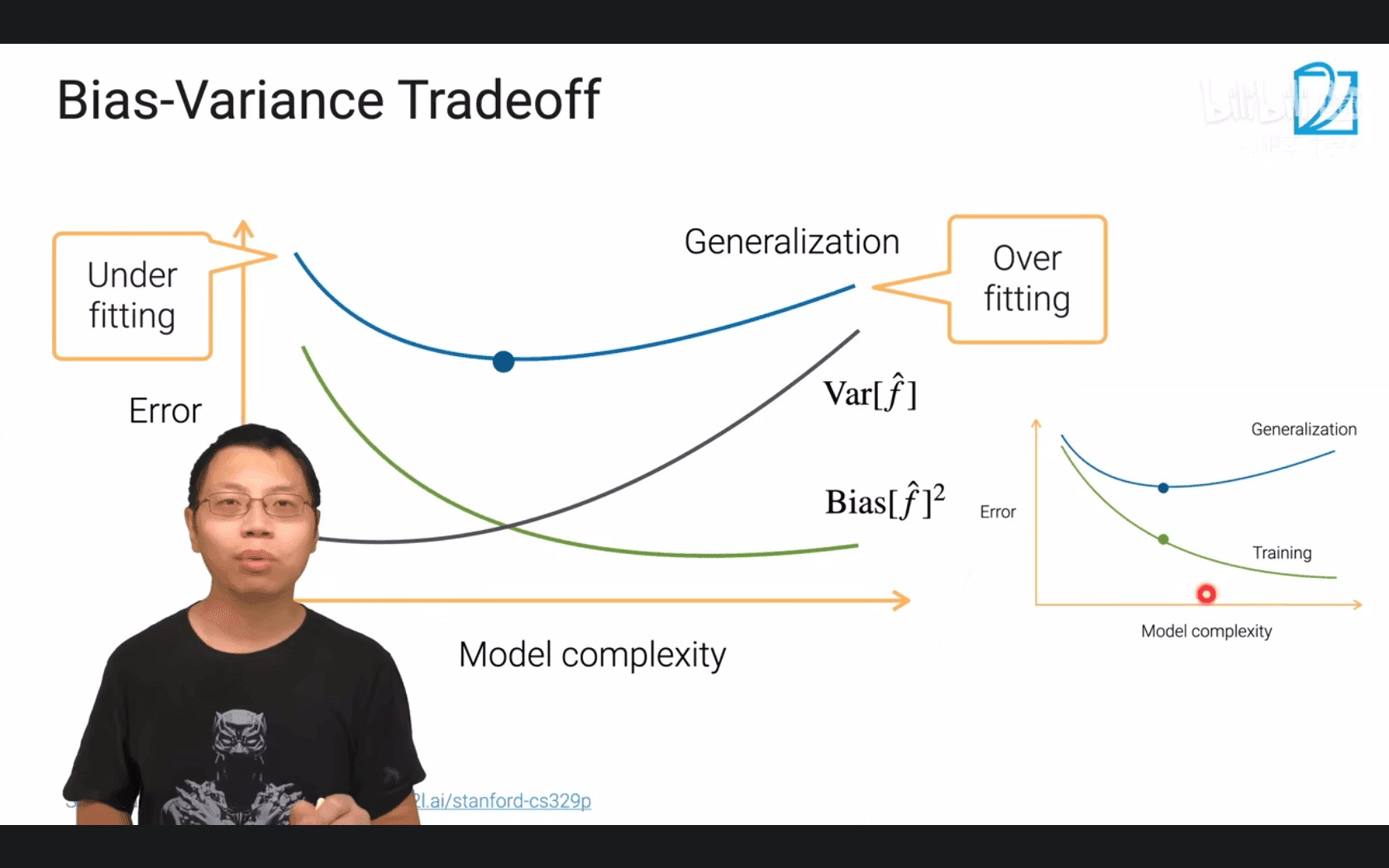
4.2 过拟合和欠拟合
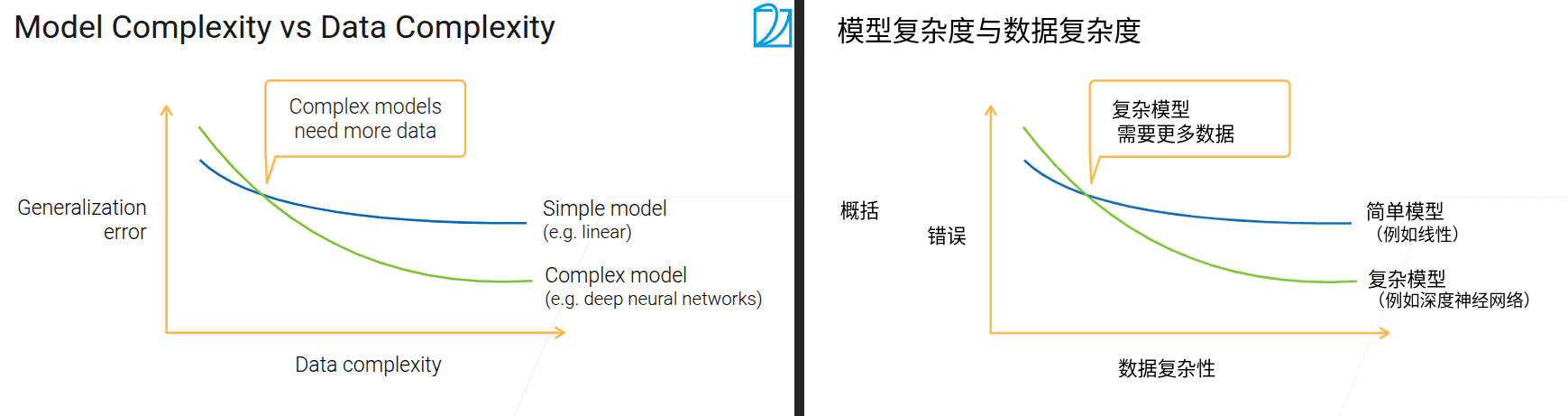
- 是用模型去拟合数据,所以他们两个的复杂性要对等
- 最好的点是泛化误差最低的时候
- 最好的情况下也可能存在过拟合
- 当增加数据复杂度,模型的泛化误差不再下降时,因该考虑换更复杂的模型
- 对于工业界,在没有太大样本的情况下因该先考虑小模型
- 当数据逐渐积累,跨过交点之后,就因该开始升级模型;数据和模型要是一个相互匹配的过程
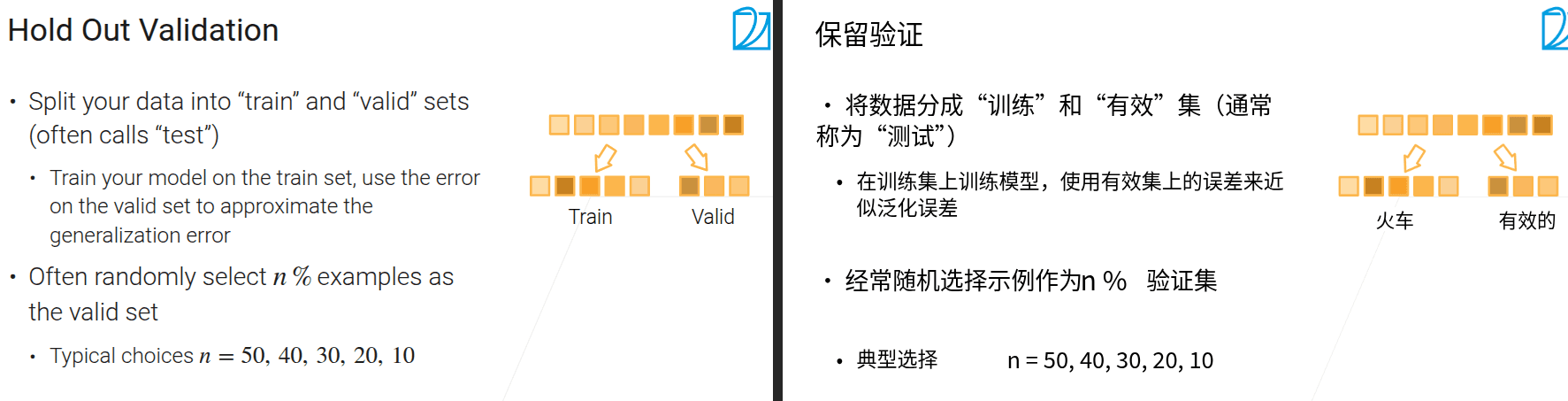
4.3 模型验证
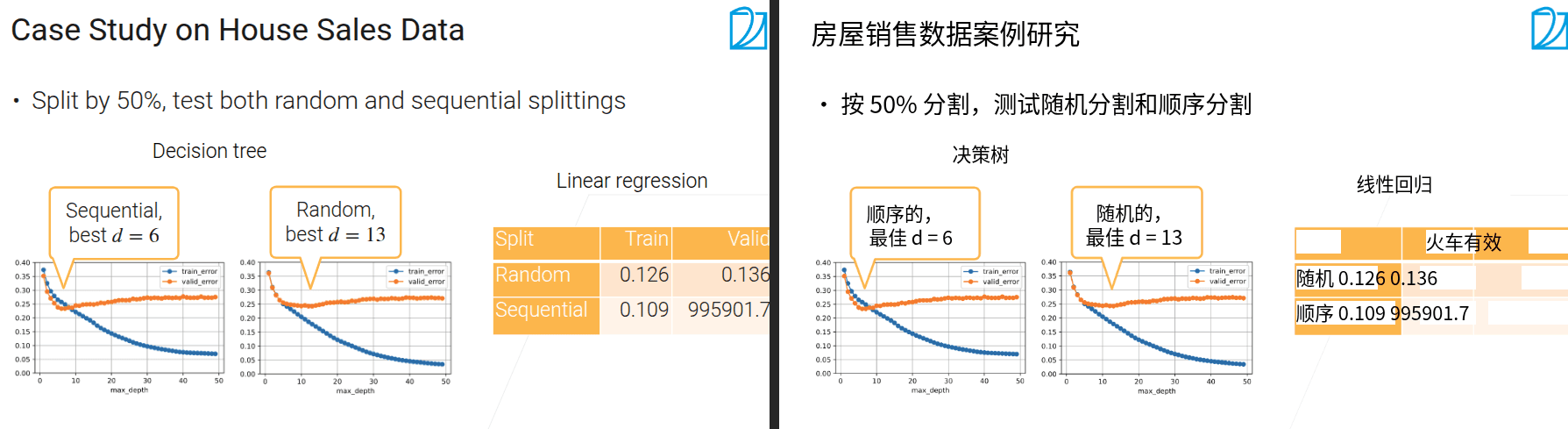
- 随机切分数据集的前提是数据的每个样本是符合独立同分布的
- IID 是 独立同分布(Independent and Identically Distributed) 的缩写。
- 针对时序数据、最好要保证验证样本在驯练样本之后
- 对于组信息,先把组分开,不要一个组的信息既在测试又在验证,会导致准确度偏高
-
K折交叉验证是一种在数据量有限时很有用的模型评估方法。它将训练数据分成\(K\)个不重叠的部分,然后进行\(K\)轮训练与验证:每一轮用其中\(K - 1\)个部分作为训练集来训练模型,剩下的1个部分作为验证集评估模型性能;最后将\(K\)轮的验证误差取平均,得到对模型泛化能力更稳定的评估结果。常见的\(K\)值选择为5或10。并且,每一轮的模型都是基于该轮特定的训练集重新训练的,各轮的模型训练和评估过程相互独立,能有效避免因单次数据划分随机导致的评估偏差,更全面地反映模型在不同数据子集上的表现。
- 数据集比较少的时候可以取更大的K

5.1 方差和偏差
- 偏差 学习到的模型和真实模型之间的区别、位移
-
这个式子太清晰,白话:你的模型既要准也要稳定,真实标签的噪声不是你能掌握的
- 目标是从采样到的D中学习\(\hat{f}\),使得\(\hat{f}\)与真实f尽可能的相近
- 通过期望E(泛化误差)来衡量模型在不同情况下的表现
- 偏差+方差+噪音



在机器学习中,Bias(偏差) 和 Variance(方差) 是衡量模型性能的两个核心概念,用于描述模型的拟合能力和泛化能力,二者共同构成了模型的预测误差(误差 = 偏差² + 方差 + 不可避免的噪声)。
1. Bias(偏差):模型的“拟合能力缺陷”
- 定义:偏差是模型对训练数据的平均预测值与真实值之间的差距,反映了模型对问题本质规律的捕捉能力。
- 本质:偏差源于模型的“简化假设”——当模型过于简单(如线性模型拟合非线性数据),无法捕捉数据的真实模式时,会产生高偏差。
- 表现:
- 高偏差:模型“欠拟合”(Underfitting),对训练数据和新数据的预测都不准确(如用直线拟合曲线分布的数据)。
- 低偏差:模型能较好地捕捉数据规律(如复杂的多项式模型、深度神经网络)。
2. Variance(方差):模型的“稳定性缺陷”
- 定义:方差是模型对不同训练数据集的预测结果之间的波动程度,反映了模型对训练数据中随机噪声的敏感程度。
- 本质:方差源于模型的“过度复杂”——当模型过于灵活(如高阶多项式、过深的神经网络),会过度学习训练数据中的细节(包括噪声),导致对不同训练子集的预测结果差异很大。
- 表现:
- 高方差:模型“过拟合”(Overfitting),对训练数据预测极准,但对新数据(测试集)预测误差很大(如记住了训练数据的随机波动)。
- 低方差:模型对不同训练数据的预测结果稳定(如简单的线性模型)。
3. 偏差-方差权衡(Bias-Variance Tradeoff)
- 模型的复杂度与偏差、方差通常呈“此消彼长”的关系:
- 简单模型(如线性回归):高偏差、低方差(欠拟合风险)。
- 复杂模型(如深度学习):低偏差、高方差(过拟合风险)。
- 机器学习的核心目标之一,就是找到偏差和方差的平衡点,使模型在训练数据和新数据上的表现都较好(泛化能力强)。
- 解决高偏差:增加模型复杂度(如添加特征、使用非线性模型)。
- 解决高方差:降低模型复杂度(如正则化、减少特征、增加训练数据)。
举例说明
- 用“射击打靶”类比:
- 高偏差:子弹集中在靶心外侧(模型整体偏离真实规律)。
- 高方差:子弹分散在靶心周围(模型对不同数据波动敏感)。
- 理想状态:子弹密集在靶心(低偏差+低方差)。
理解偏差和方差,有助于诊断模型问题(欠拟合/过拟合)并针对性优化。
5.2 Bagging
- 主要效果是能降低方差,特别是在模型不稳定的时候效果更加明显
-
最重要的应用是随机森林
要理解Bagging(装袋)方法的数学原理,我们可以从方差减少和期望不等式这两个核心点来拆解:
1. Bagging的核心逻辑:“集体智慧”降低方差
Bagging是一种集成学习方法,核心思想是:
- 用有放回抽样(Bootstrap)生成多个不同的训练子集;
- 对每个子集训练一个“基础学习器”(比如决策树,这类学习器对数据变化很敏感,属于“不稳定学习器”);
- 最终预测时,对所有基础学习器的结果取平均(回归任务)或投票(分类任务)。
之所以有效,是因为单个不稳定学习器的方差大(数据稍变,模型就大改),但多个学习器“集体决策”时,方差会被平均抵消,从而让整体模型更稳定。
2. 数学推导:用期望不等式证明“方差减少”
我们用回归任务来具体推导(分类任务可类似理解):
符号定义
- $ f(x) $:数据的“真实标签”(ground truth,理想中完美的预测);
- $ \hat{f}_D(x) \(:单个基础学习器的预测(\) D $ 代表这个学习器是基于某一个Bootstrap抽样子集训练的);
- $ \hat{f}(x) \(:Bagging的最终预测,即所有基础学习器预测的**期望**:\) \hat{f}(x) = \mathbb{E}_D\left[ \hat{f}_D(x) \right] $(对所有可能的Bootstrap子集 $ D $ 取平均)。
关键不等式:$ \mathbb{E}[X]^2 \leq \mathbb{E}[X^2] $
这个不等式叫“柯西 - 施瓦茨不等式”的特例,也可以从“方差非负”推导: 方差 $ \text{Var}(X) = \mathbb{E}[X^2] - \left( \mathbb{E}[X] \right)^2 \geq 0 $,因此必然有 $ \left( \mathbb{E}[X] \right)^2 \leq \mathbb{E}[X^2] $。
推导“Bagging的误差 ≤ 单个学习器的误差期望”
我们要比较 Bagging的预测误差 和 单个基础学习器的误差期望:
- Bagging的预测误差:$ \left( f(x) - \hat{f}(x) \right)^2 $(真实值与Bagging最终预测的差距);
- 单个基础学习器的误差期望:$ \mathbb{E}_D\left[ \left( f(x) - \hat{f}_D(x) \right)^2 \right] $(对所有可能的Bootstrap子集 $ D $,单个学习器误差的平均)。
我们需要证明: $ \left( f(x) - \hat{f}(x) \right)^2 \leq \mathbb{E}_D\left[ \left( f(x) - \hat{f}_D(x) \right)^2 \right] $
推导步骤: 展开右边的期望: $$ \begin{align} \mathbb{E}_D\left[ \left( f(x) - \hat{f}_D(x) \right)^2 \right] &= \mathbb{E}_D\left[ \left( (f(x) - \hat{f}(x)) + (\hat{f}(x) - \hat{f}_D(x)) \right)^2 \right] \ &= \mathbb{E}_D\left[ (f(x) - \hat{f}(x))^2 + 2(f(x) - \hat{f}(x))(\hat{f}(x) - \hat{f}_D(x)) + (\hat{f}(x) - \hat{f}_D(x))^2 \right] \end{align} $$
对这个式子取期望后,中间项 $ 2(f(x) - \hat{f}(x))(\hat{f}(x) - \hat{f}_D(x)) $ 的期望为 $ 0 $(因为 $ \hat{f}(x) = \mathbb{E}_D[\hat{f}_D(x)] $,所以 $ \mathbb{E}_D[\hat{f}(x) - \hat{f}_D(x)] = 0 $)。因此: $$ \mathbb{E}_D\left[ \left( f(x) - \hat{f}_D(x) \right)^2 \right] = \left( f(x) - \hat{f}(x) \right)^2 + \mathbb{E}_D\left[ (\hat{f}(x) - \hat{f}_D(x))^2 \right] $$
由于方差项 $ \mathbb{E}_D\left[ (\hat{f}(x) - \hat{f}_D(x))^2 \right] \geq 0 $,因此: $$ \left( f(x) - \hat{f}(x) \right)^2 \leq \mathbb{E}_D\left[ \left( f(x) - \hat{f}_D(x) \right)^2 \right] $$
这就证明了:Bagging的预测误差,小于等于“单个基础学习器误差的期望”——换句话说,Bagging让模型的整体误差(方差主导的部分)降低了。
总结
Bagging的数学本质是:通过“多个不稳定学习器的平均/投票”,利用期望不等式和方差平均抵消的原理,让集成后的模型比单个学习器更稳定(方差更小),从而提升预测精度。
5.3 Boosting
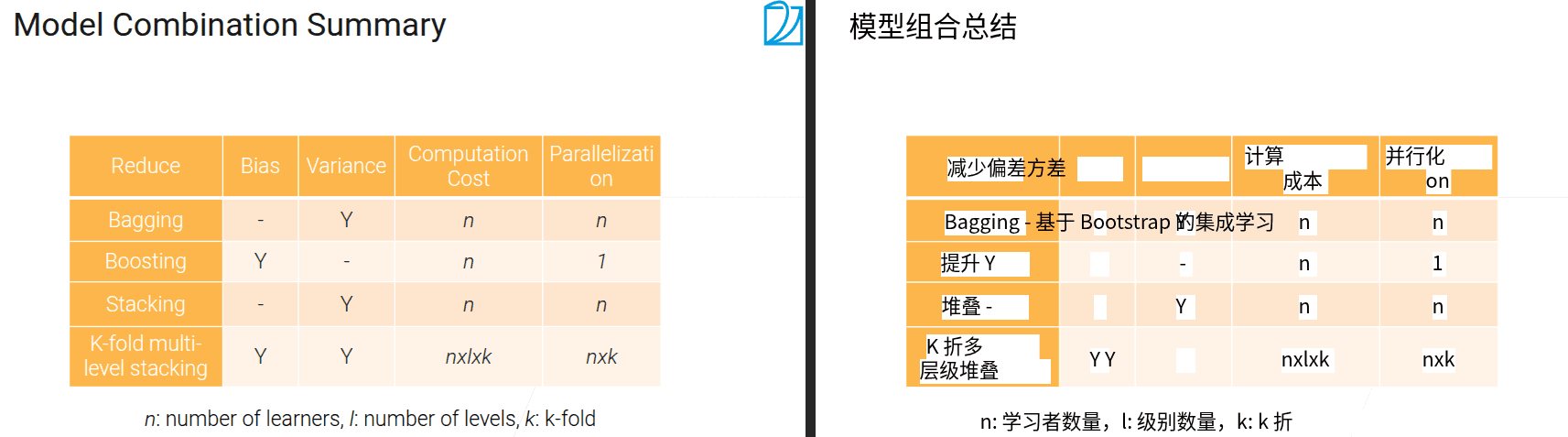
- 将多个弱模型组合在一起变成一个强的模型。主要目的是去降低偏差,而不是方差(bagging降低方差
- boosting按顺序学习模型,bagging的话每个模型是独立的
- boosting专注于学习上一个模型预测失败的部分
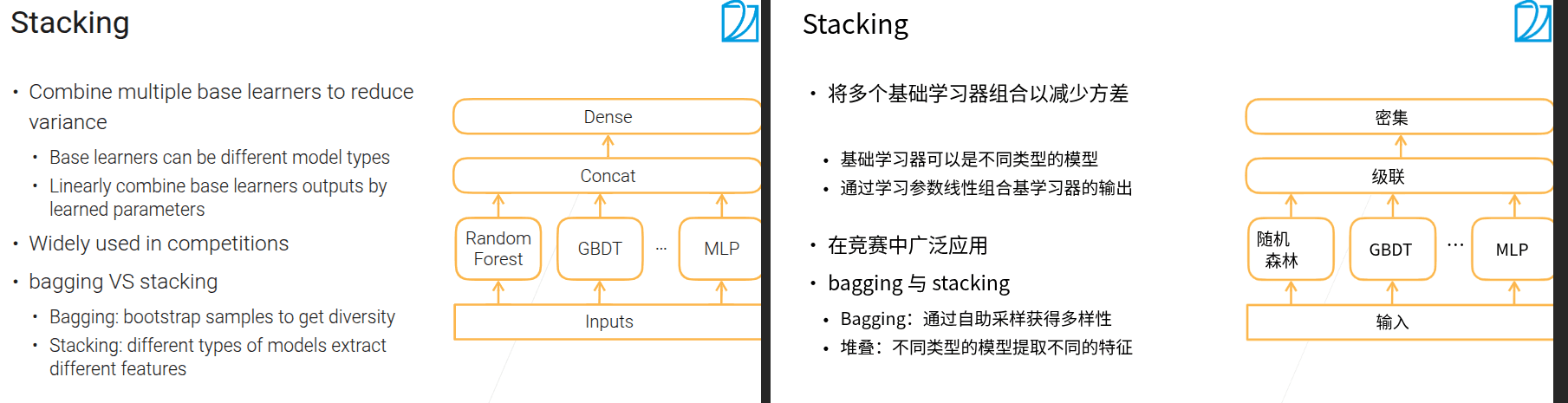
5.4 Stacking
- 类似bagging,用于降低方差,区别是可以用不同的模型类别
- bagging在不同数据上训练相同的模型
- stacking在相同数据上训练不同的模型。种类不一样,所以差别很大,以此来降低方差
-
stacking的准则
- 新模型加入能提升精度
-
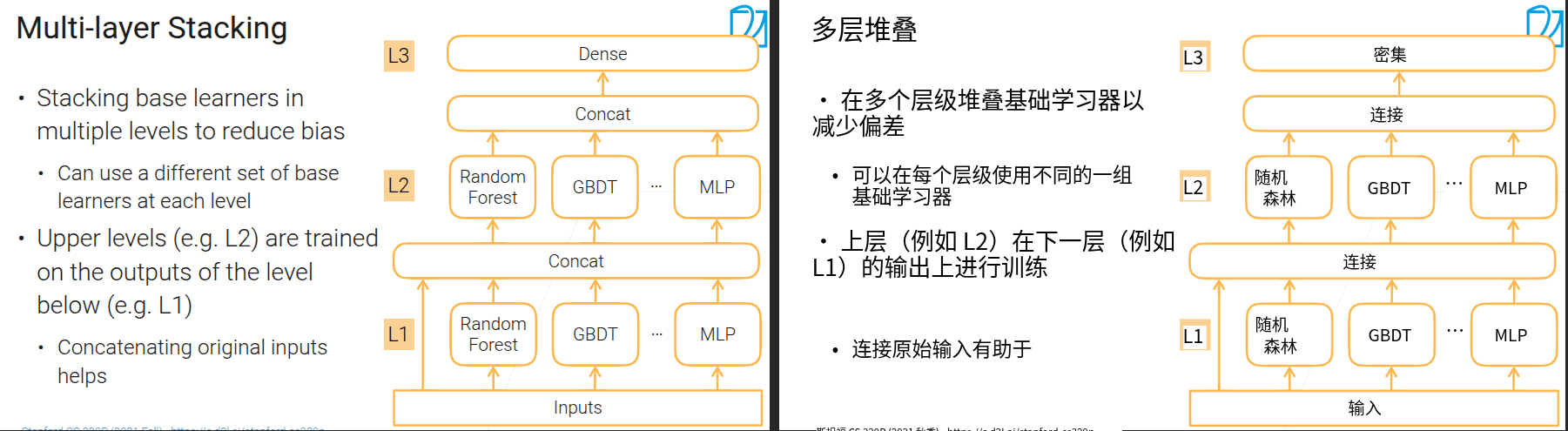
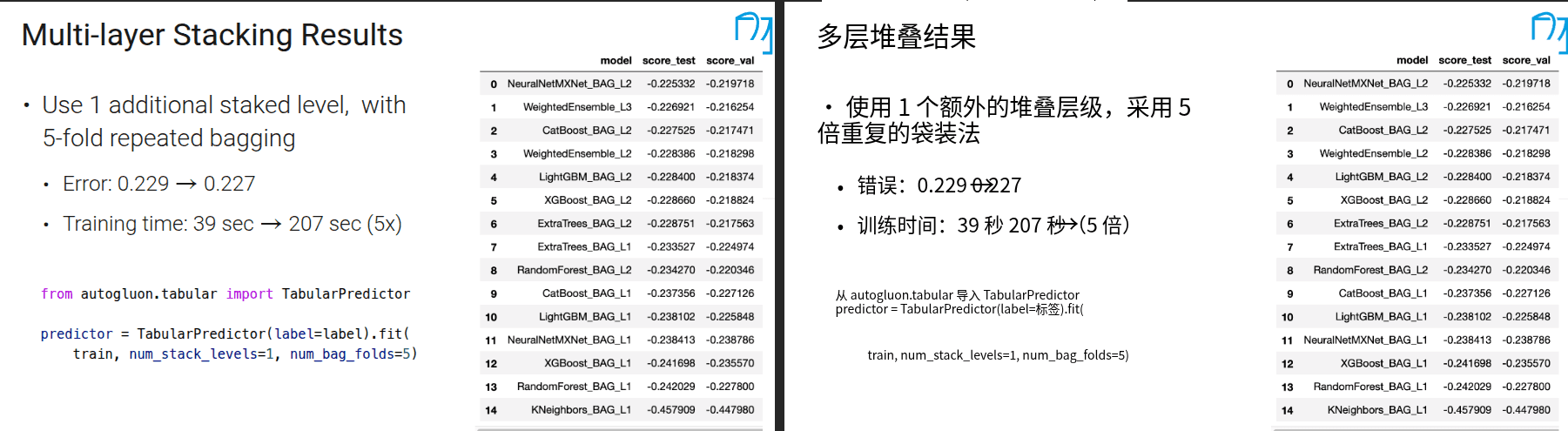
stacking可以通过一些方法降低偏差
- 多层stacking特别容易过拟合
9.1 模型调参
- 要注意的是,每次只调一个值
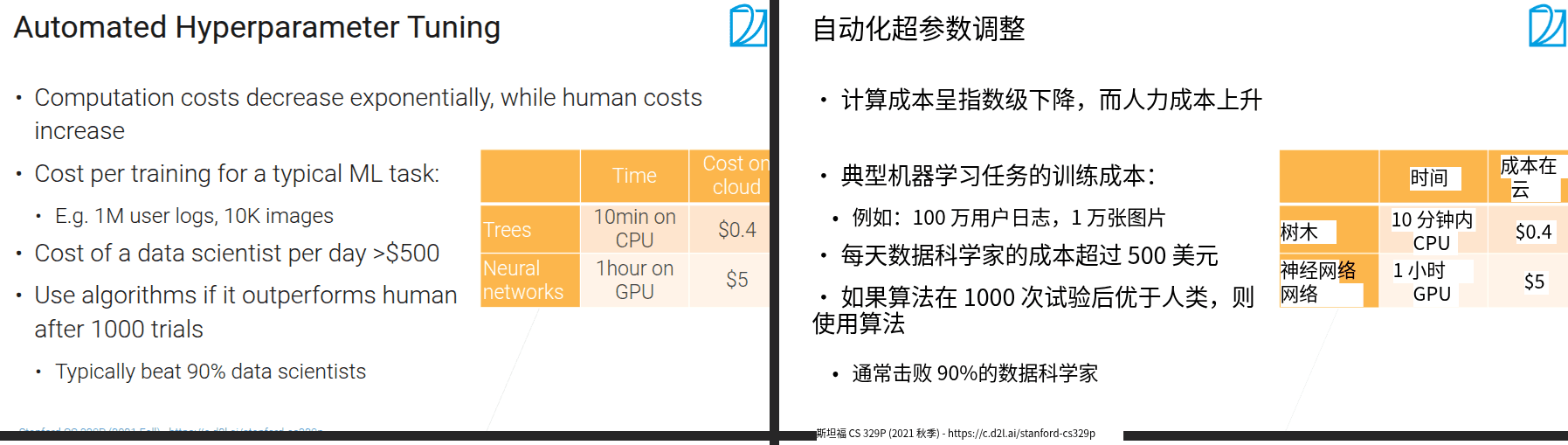
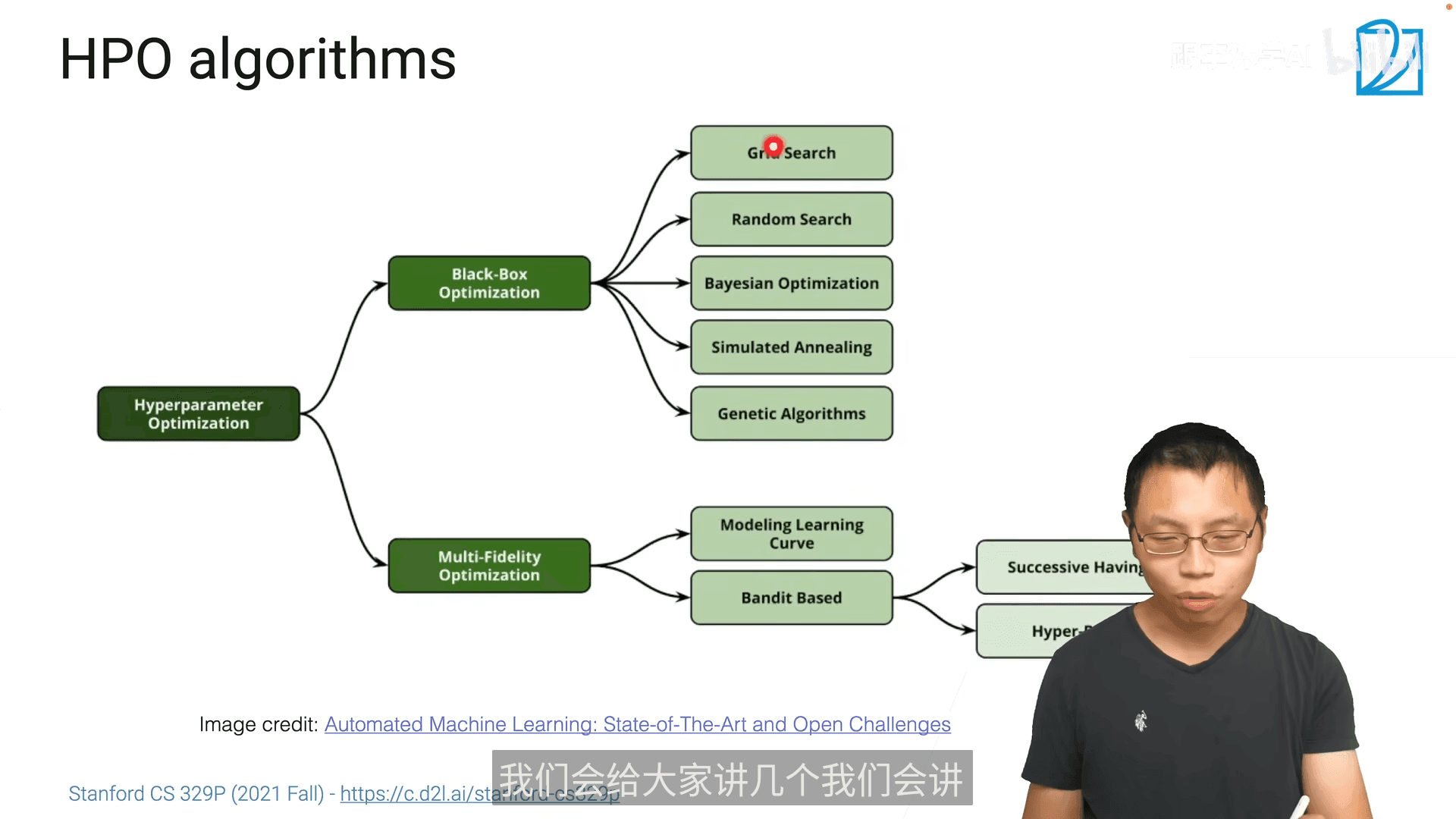
9.2 超参数优化(HPO)
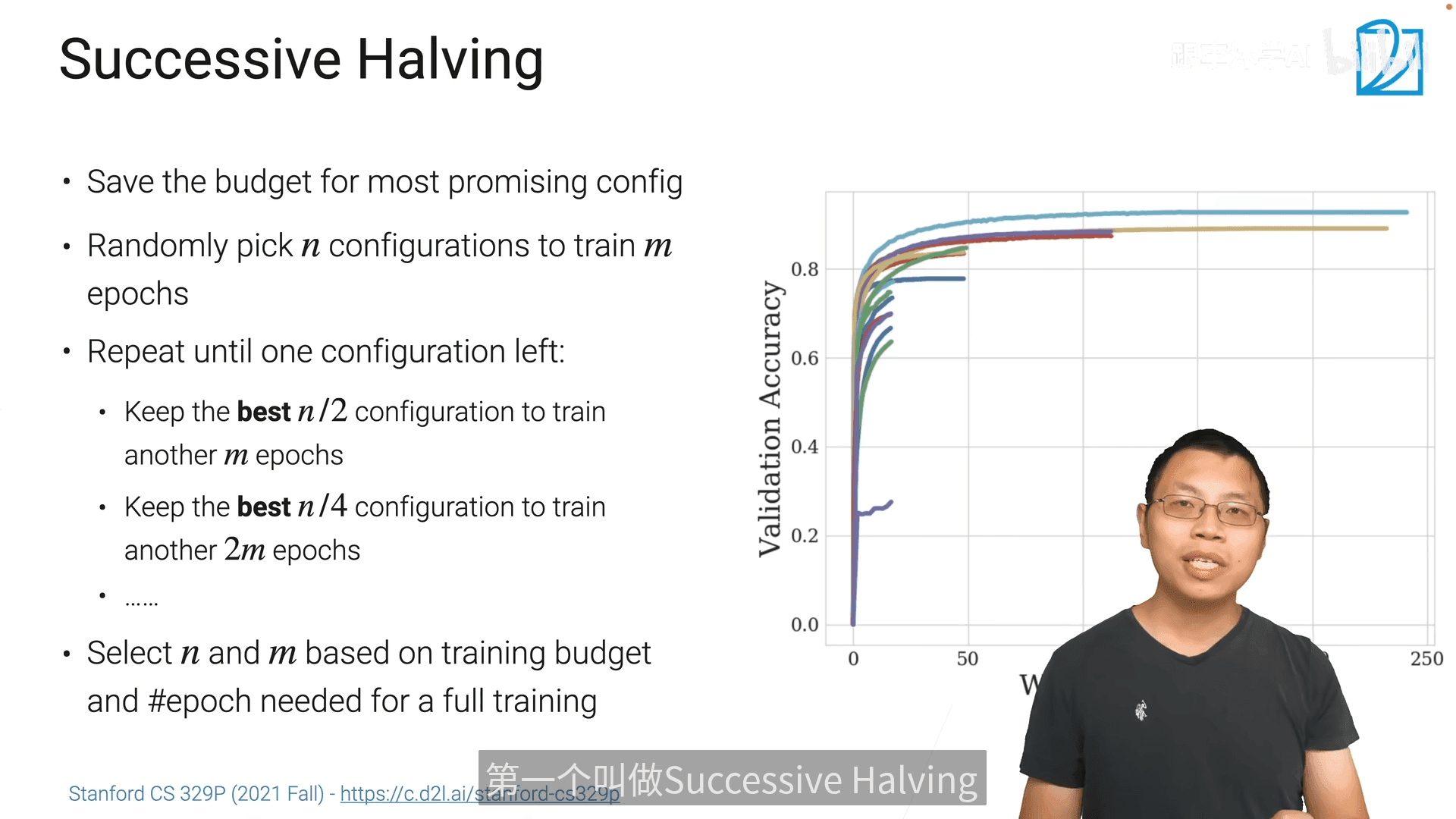
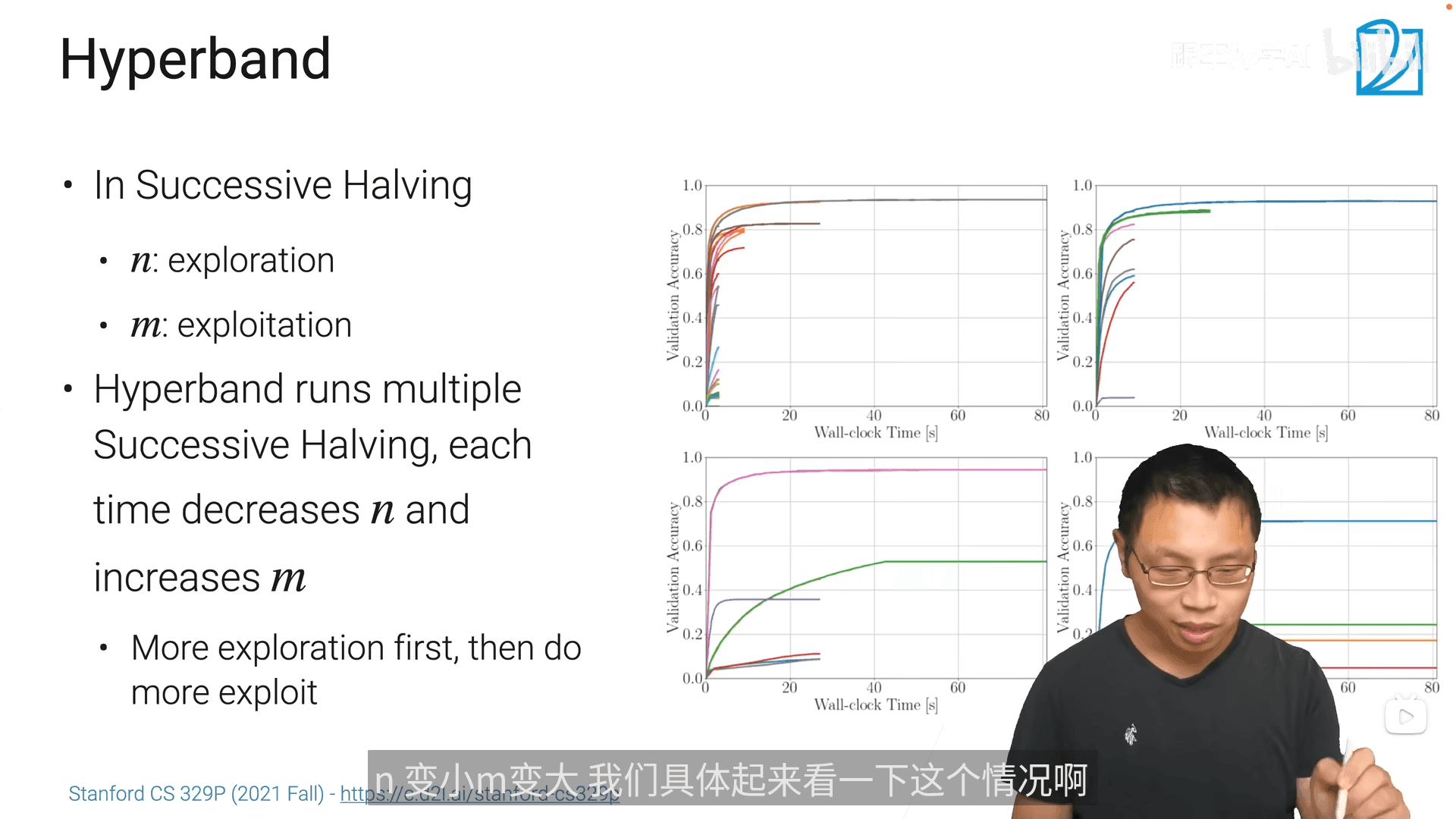
多保真度超参数优化(Multi-Fidelity HPO)使用较多
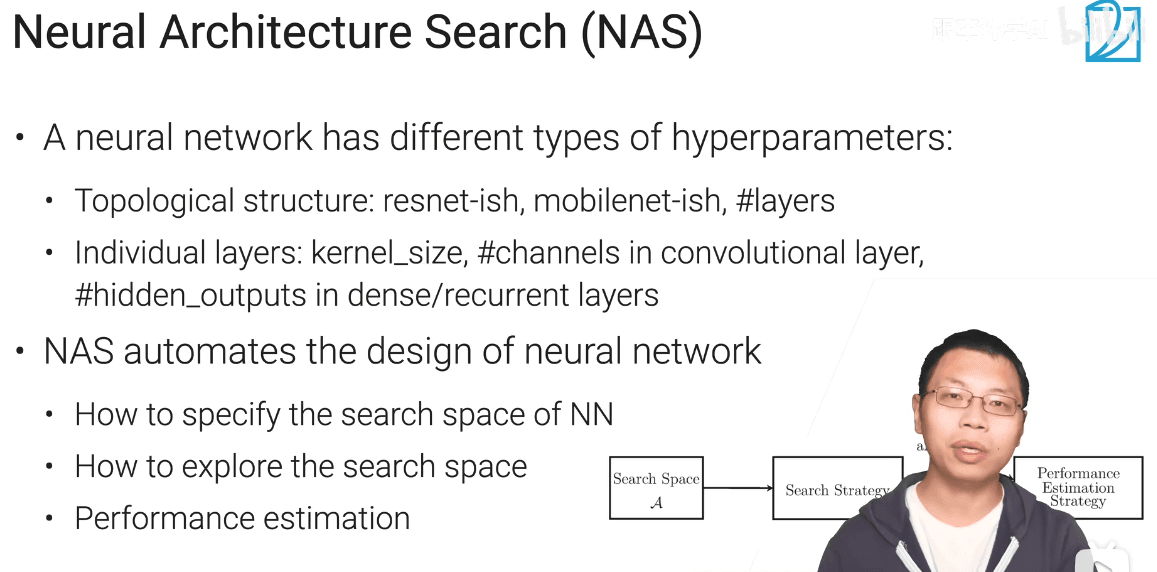
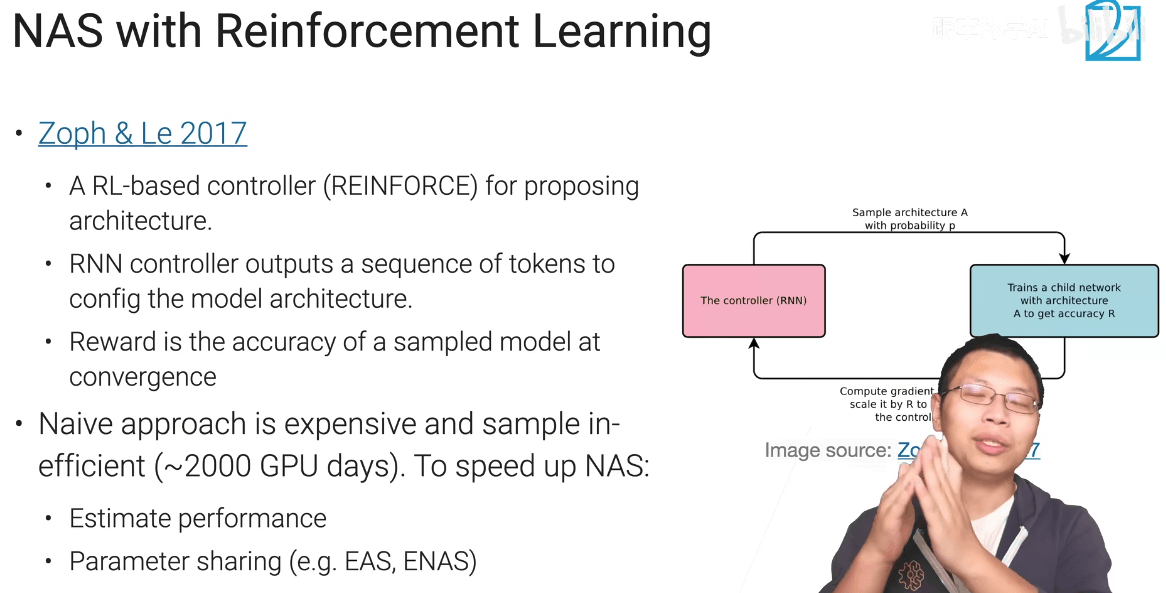
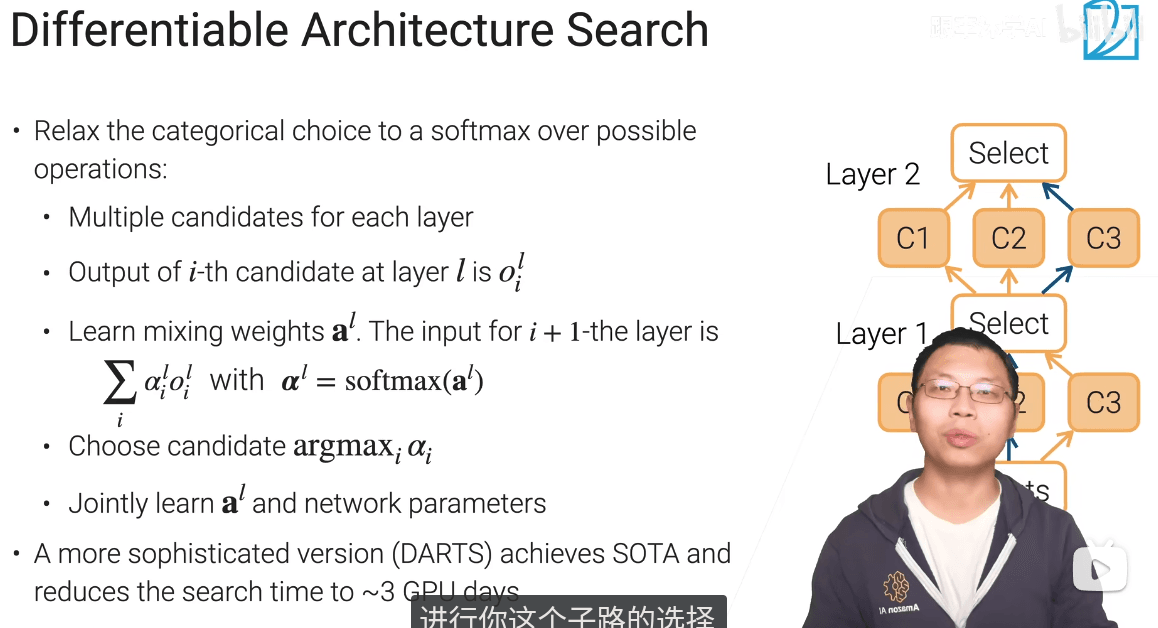
9.3 网络架构搜索(NAS)
10.1 深度神经网络架构
- 本章关于DNN中的一些共用的设计模式
- 各种归一化
- 残差连接
- 注意力机制
-DNN是一种编程语言。和一般语言不一样的地方是有很多不固定的参数,是通过真实数据得到的
- 使训练更简单。损失函数更加平滑(导数值的变化更加平滑),可以用更大的学习率
- 对DNN没有帮助,只会帮助直接线性作用在X上的这个函数,但是DNN有许多非线性层
- 应用BN可以使用更大的学习率,同时不会改变最后的结果

- 还原是可学习的
首先直接说结论:Recovery(恢复)这一步是为了让BatchNorm保留模型的表达能力,避免标准化后丢失原数据的特征分布信息。
具体解释
-
标准化的“副作用”: 标准化(\(\hat{\mathbf{x}}'_j = (\mathbf{x}'_j - \text{mean}(\mathbf{x}'_j))/\text{std}(\mathbf{x}'_j)\))会把数据强行拉到“均值0、方差1”的分布,但这可能会抹掉原数据中对模型有用的特征(比如某些特征本身就该有较大的方差或偏移)。
-
Recovery的作用: 这一步通过可学习的参数 \(\gamma_j\)(缩放因子)和 \(\beta_j\)(偏移因子),让模型自己调整标准化后的数据分布:
- \(\gamma_j\) 控制“方差”:如果原特征的大方差是有用的,模型可以把 \(\gamma_j\) 调大,恢复(甚至增强)方差;
- \(\beta_j\) 控制“偏差(均值)”:如果原特征的均值偏移是有用的,模型可以把 \(\beta_j\) 调偏,恢复(甚至调整)均值。
简单说:标准化是为了“稳定训练”,而Recovery是为了“不丢信息”——让模型既能享受标准化带来的训练便利,又能保留原数据的有效特征分布~
要不要我帮你整理一份BatchNorm完整步骤的简化笔记?
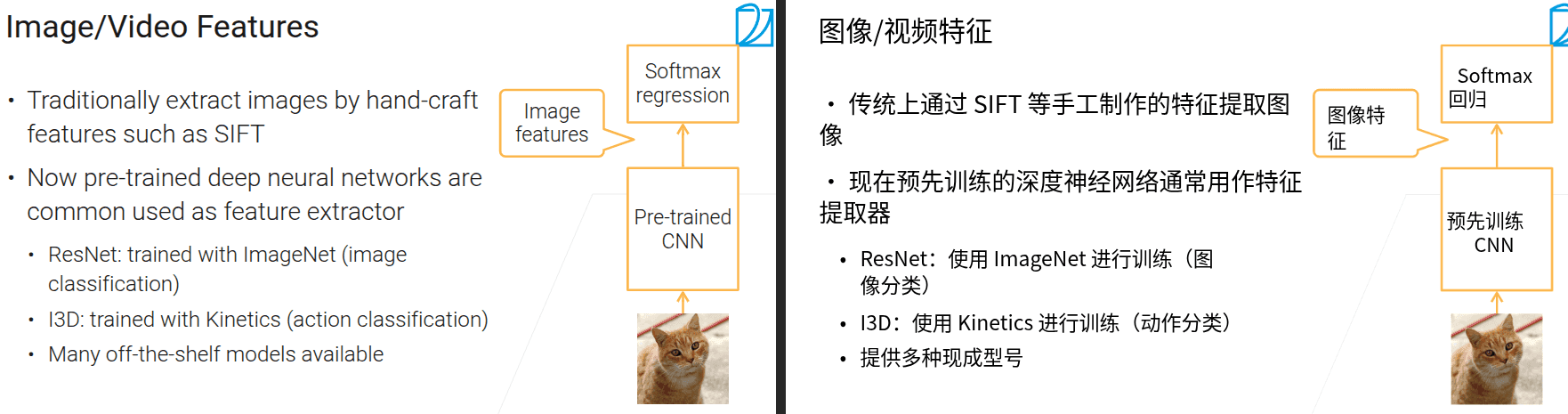
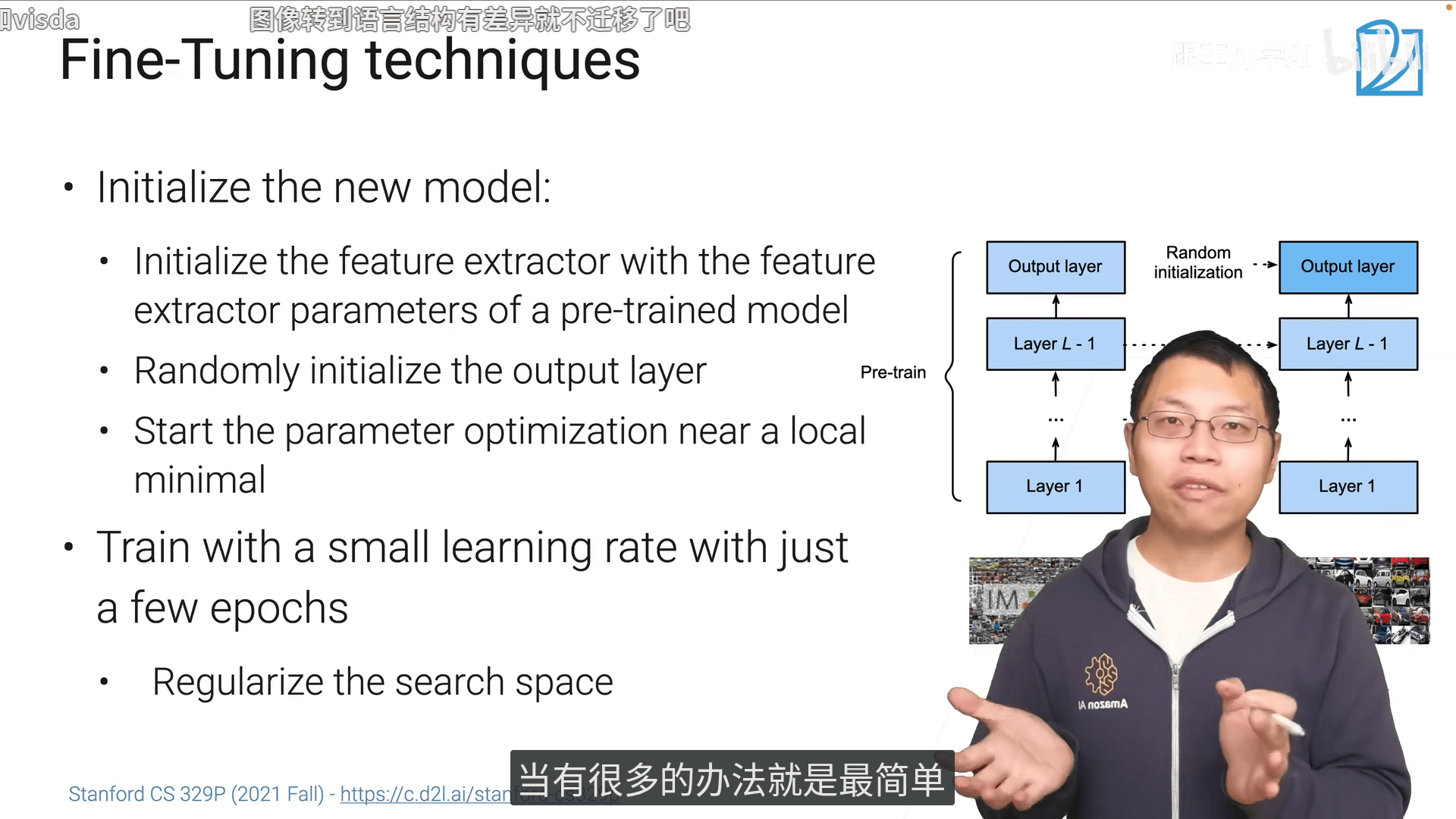
11.1 迁移学习
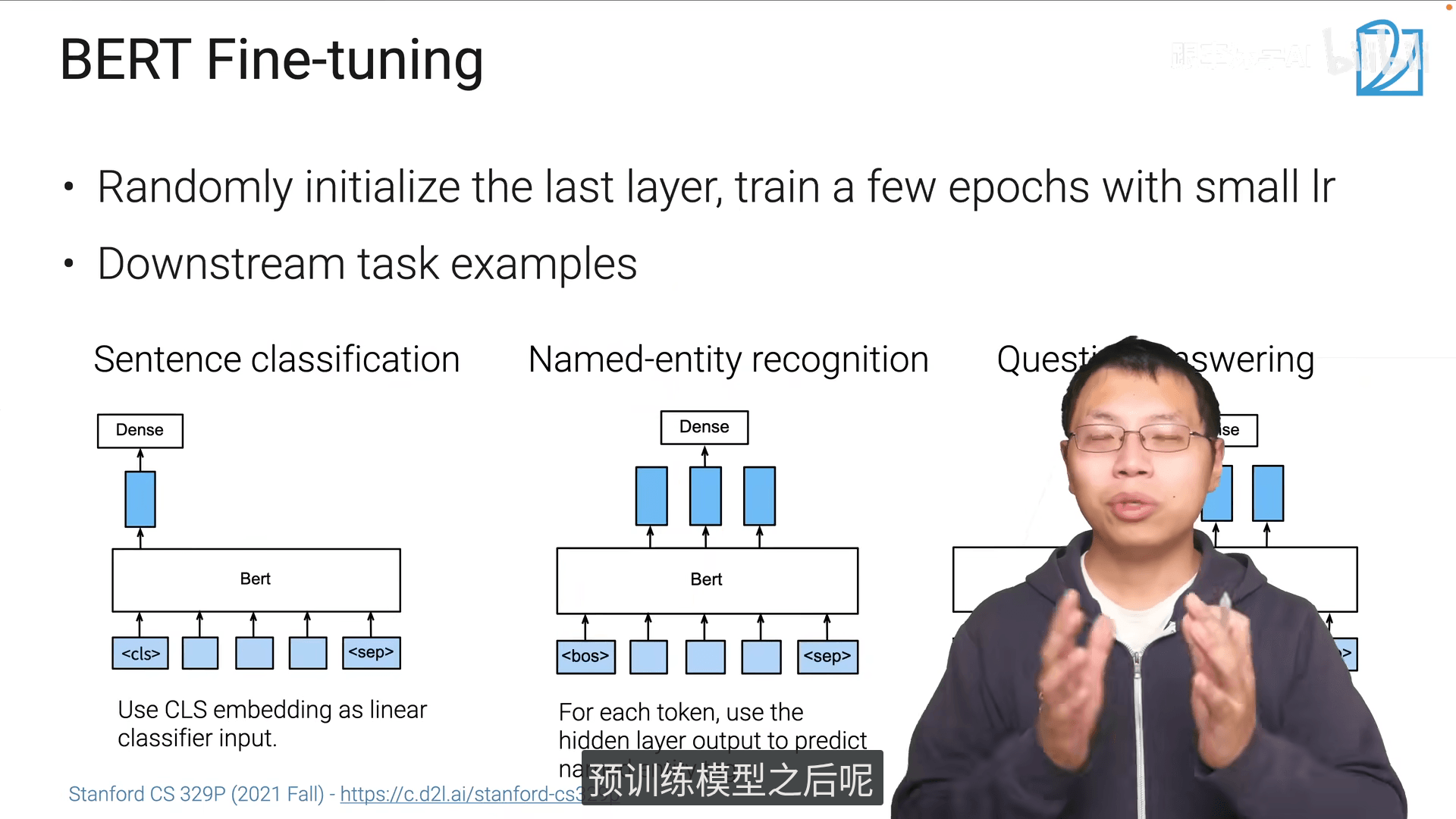
11.2 NLP中的微调
summary
课程包括了ML从数据获取->数据清洗->模型架构选择->训练效果评估->参数调优